Uniformni polihoron


Uniformni polihoron je v geometriji polihoron ali 4-politop, ki je ogliščno prehoden. Njegove celice so uniformni poliedri.
Zgodovina odkritij
uredi- Pravilni politopi (konveksne stranske ploskve)
- Leta 1852 je Ludwig Schläfli (1814-1895) v svojem rokopisu Theorie der vielfachen Kontinuitet dokazal, da obstaja natančno 6 pravilnih politopov v štirih razsežnostih in samo 3 v petih ali več razsežnostih.
- pravilni zvezdni polihoroni (celice zvezdnega poliedra in/ali slike oglišč)
- Leta 1852 je Ludwig Schläfli našel štiri od desetih zvezdnih polihoronov
- Leta 1883 je Edmund Hess (1843–1903) izpopolnil seznam desetih nekonveksnih polihoronov v knjigi Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder
- Konveksni polpravilni politopi (različne definicije preden je Coxeter določil uniformno kategorijo)
- Leta 1900 je Thorold Gosset (1869-1962) oštevilčil v seznamu neprizmatičnih polpravilnih konveksnih politopov s pravilnimi celicami (platonska telesa) v svoji publikaciji On the Regular and Semi-Regular Figures in Space of n Dimensions.[1]
- Leta 1910 Alicia Boole Stott (1860–1940) v svoji publikaciji Geometrical deduction of semiregular from regular polytopes and space fillings razširila definicijo s tem, da je dovolila arhimedska telesa in celice prizem. Takšen način obravnavanja je štel 45 polpravilnih polihoronov.[2]
- Leta 1911 je Pieter Hendrik Schoute (1846-1923) objavil delo Analytic treatment of polytopes regulary derived from the regular polytopes. Temu je sledilo oštevilčenje konveksnih uniformnih politopov s simetrijo osnovano na 5 celici, 8 celici, 16 celici in 24 celici.
- Leta 1912 je Emanuel Lodewijk Elte razširil Gossetov seznam z objavo dela The Semiregular Polytopes of the Hyperspaces z enim ali dvema vrstama polpravilnih facet.
- Konveksni uniformni politopi
- Leta 1940 so se raziskave sistematično nadaljevale z delom Harolda Scotta MacDonalda Coxeterja (1907–2003)v njegovi publikaciji Regular and Semi-Regular Polytopes
- Konveksni uniformni polihoroni
- Leta 1940 so se raziskave sistematično razširile z delom Harolda Scotta MacDonald Coxeterja v njegovi knjigi Regular and Semi-Regular Polytopes.
- Leta 1965 je bil dokončno izdelan seznam konveksnih oblik, ki sta ga pripravila John Horton Conway (rojen 1937) in Michael Guy (rojen 1942) v njuni publikaciji.
- Leta 1966 je matematik Norman Johnson (rojen 1930) dokončal svojo doktorsko dizertacijo
- Leta 1997 je George Olshevsky (rojen 1946) podal poln seznam in imena ter elemente konveksnih polihoronov
- Leta 2004 je izšel dokaz, da je Conway-Guyeva množica popolna, kar je oblavil Marco Möller v svoji dizertaciji Vierdimensionale Archimedische Polytope.[3]
- Leta 1940 so se raziskave sistematično nadaljevale z delom Harolda Scotta MacDonalda Coxeterja (1907–2003)v njegovi publikaciji Regular and Semi-Regular Polytopes
- Nepravilni uniformni zvezdni polihoroni (podobni so nekonveksnim uniformnim poliedrom)
- Pot naprej Znanih je na tisoče nekonveksnih polihoronov, toda večina od njih je neobjavljenih. Tudi njihov seznam verjetno še ni popoln. Prav tako ni ocen kako dolg bi naj bil popoln seznam. Med najbolj znanimi raziskovalci na tem področju so Jonathan Bowers (rojen 1969 [4]), George Olshevsky (rojen 1946) in Norman Johnson (rojen 1930).
Pravilni polihoroni
urediUniformni polihoroni vključujejo dve posebni podskupini, ki zadoščata dodatnim zahtevam:
- 16 pravilnih polihoronov z lastnostjo, da so vse celice, stranske ploskve robovi in oglišča skladni
Konveksni uniformni polihoroni
uredi
Za ta zgled so prikazane tri konstrukcije rektificirane 24 celice:




 ,
, 





 ,
, 





 .
.Znanih je 64 uniformnih konveksnih polihoronov, vključno s šestimi pravilnimi konveksnimi polihoroni. Sem ni šteta neskončna množica duoprizem in antiprizmatičnih hiperprizem.
- pet je poliederskih prizem osnovanih na platonskih telesih
- trinajst je poliederskih prizem osnovanih na arhimedskih telesih
- devet jih je v družini grupe pravilnih sebi dualnih A4[3,3,3] (5 celica)
- devet je članov v družini grupe pravilnih sebi dualnih F4[3,4,3] (24 celica), razen prirezane 24-celice
- petnajst jih je v družini pravilne grupe BC4 (129 celica/600 celica)
- ena posebna prirezana oblika družine v grupi [3,4,3] (24 celica)
- ena posebna ne-Wythoffov polihoron , velika antiprizma
- Skupaj je to 68 – 4 = 64
Teh 64 polihoronov je indeksiral izdajatelj, pisec in založnik George Olshevsky (rojen 1946).
Skupina A4
uredi5-celica ima diploidno pentahorsko [3,3,3] simetrijo z redom 120, izomorfnih s permutacijami petih elementov, ker so vsi pari oglišč povezani na isti način. V spodnjem seznamu so tri oblike označene z *. Te imajo višjo razširjeno pentahorsko simetrijo reda 240, [[3,3,3]] ker se elementi, ki pripadajo osnovni 5-celici, lahko zamenjajo z enim od tistih, ki odgovarjajo elementom duala.
Facete (celice) so podane in razvrščene v skupine v svojih Coxeter-Dinkinovih lokacijah z odstranitvijo določenih vozlov.
| # | Johnsonovo ime Bowersovo ime (in okrajšava) |
slika oglišč |
Coxeter-Dinkinov in Schläflijevi simboli |
Število celic po položaju | Število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| položaj 3 (5) |
položaj 2 (10) |
položaj 1 (10) |
položaj 0 (5) |
celice | stranske ploskve | robovi | oglišča | ||||
| 1 | 5 celica pentahoron (pen) |

|
{3,3,3} |
(4) (3.3.3) |
5 | 10 | 10 | 5 | |||
| 2 | rektificirana 5 celica rektificirani pentahoron (rap) |

|
t1{3,3,3} |
(3) (3.3.3.3) |
(2) (3.3.3) |
10 | 30 | 30 | 10 | ||
| 3 | prisekana 5 celica prisekani pentahoron (tip) |

|
t0,1{3,3,3} |
(3) (3.6.6) |
(1) (3.3.3) |
10 | 30 | 40 | 20 | ||
| 4 | kantelirana 5 celica mali rombski pentahoron (srip) |

|
t0,2{3,3,3} |
(2) (3.4.3.4) |
(2) (3.4.4) |
(1) (3.3.3.3) |
20 | 80 | 90 | 30 | |
| 5 | *runcinirana 5 celica mali prizmatični dodekaeder (spid) |

|
t0,3{3,3,3} |
(1) (3.3.3) |
(3) (3.4.4) |
(3) (3.4.4) |
(1) (3.3.3) |
30 | 70 | 60 | 20 |
| 6 | *dvojno prisekana 5 celica dekakron (deca) |

|
t1,2{3,3,3} |
(2) (3.6.6) |
(2) (3.6.6) |
10 | 40 | 60 | 30 | ||
| 7 | kantiprisekana 5 celica veliki rombski pentahoron (grip) |

|
t0,1,2{3,3,3} |
(2) (4.6.6) |
(1) (3.4.4) |
(1) (3.6.6) |
20 | 80 | 120 | 60 | |
| 8 | runciprisekana 5 celica prizemskorombski pentahoron (prip) |

|
t0,1,3{3,3,3} |
(1) (3.6.6) |
(2) (4.4.6) |
(1) (3.4.4) |
(1) (3.4.3.4) |
30 | 120 | 150 | 60 |
| 9 | *omniprisekana 5 celica veliki prizmatični dekahoron (gippid) |

|
t0,1,2,3{3,3,3} |
(1) (4.6.6) |
(1) (4.4.6) |
(1) (4.4.6) |
(1) (4.6.6) |
30 | 150 | 240 | 120 |
Grafi
urediTri Coxeterjeve ravnine dvorazsežne projekcije so dane za A4, A3, A2 Coxeterjeve grupe, ki kažejo simetrijo reda 5,4,3 ter so podvojene za parne Ak rede na 10, 4, 6 za simetrične Coxeterjeve diagrame.
Trirazsežne slike so narisane kot projekcije Schleglovih diagramov usredinjenih na celice na položaju 3, s pravilno orientacijo in petimi celicami na položaju 0 kot je prikazano.
| # | Johnsonovo ime Bowersovo ime (in okrajšava) |
Coxeter-Dinkinov diagram in Schläflijevi simboli |
Coxeterjev element#Coxeterjeva ravnina grafi | Schleglov diagram | |||
|---|---|---|---|---|---|---|---|
| A4 [5] |
A3 [4] |
A2 [3] |
tetraeder usrediščen |
dualni tetraeder usrediščen | |||
| 1 | 5 celica pentahoron (pen) |
{3,3,3} |

|

|

|

| |
| 2 | rektificirana 5 celica rektificirani pentahoron (rap) |
t1{3,3,3} |

|

|

|

| |
| 3 | prisekana 5 celica prisekani pentahoron (tip) |
t0,1{3,3,3} |

|

|

|

| |
| 4 | kantelirana 5 celica mali rombski pentahoron (srip) |
t0,2{3,3,3} |

|

|

|

| |
| 5 | *runcinirana 5 celica mali prizmatičen dodekahoron (spid) |
t0,3{3,3,3} |

|

|

|

| |
| 6 | *dvojno prisekana 5 celica dekahoron (deca) |
t1,2{3,3,3} |

|

|

|

| |
| 7 | kantiprisekana 5 celica veliki rombski pentahoron (grip) |
t0,1,2{3,3,3} |

|

|

|

| |
| 8 | runciprisekana 5 celica przmatičnorombski pentahoron (prip) |
t0,1,3{3,3,3} |

|

|

|

| |
| 9 | *omniprisekana 5 celica veliki prizmatični dekahoron (gippid) |
t0,1,2,3{3,3,3} |

|

|

|

| |
Koordinate
urediKoordinate uniformnega 4-politopa s pentahorsko simetrijo se lahko generira s permutacijami celih števil v petrazsežnem prostoru s hiperravninami, ki imajo normalni vektor (1,1,1,1,1). A4 Coxeterjeva grupa je palindromska tako, da politopi obstajajo v parih dualnih oblik. Znani so trije simetrični položaji in šest parov, kar skupaj daje petnajst permutacij enega ali več kolobarjev. Vsi so navedeni spodaj v zaporedju dvojiški številski sistem zato, da je razumljivejše generiranje koordinat iz kolobarjev za vsak Coxeter-Dinkinov diagram.
Število oglišč se dobi iz permutacij števila koordinat.
| # | Osnovna točka | Ime (simetrično ime) |
Coxeter-Dinkin | oglišča |
|---|---|---|---|---|
| 1 | (0, 0, 0, 0, 1) | 5 celica | 5 | |
| 2 | (0, 0, 0, 1, 1) | rektificirana 5 celica | 10 | |
| 3 | (0, 0, 0, 1, 2) | prisekana 5 celica | 20 | |
| 4 | (0, 0, 1, 1, 1) | dvojno rektificirana 5 celica (rektificirana 5 celica) |
10 | |
| 5 | (0, 0, 1, 1, 2) | kantelirana 5 celica | 30 | |
| 6 | (0, 0, 1, 2, 2) | dvojno prisekana 5 celica | 30 | |
| 7 | (0, 0, 1, 2, 3) | kantiprisekana 5 celica | 60 | |
| 8 | (0, 1, 1, 1, 1) | trojno rektificirana 5 celica (5 celica) |
5 | |
| 9 | (0, 1, 1, 1, 2) | runcinirana 5 celica | 20 | |
| 10 | (0, 1, 1, 2, 2) | dvojno kantelirana 5 celica (kantelirana 5 celica) |
30 | |
| 11 | (0, 1, 1, 2, 3) | runciprisekana 5 celica | 60 | |
| 12 | (0, 1, 2, 2, 2) | trojno prisekana 5 celica (prisekana 5 celica) |
20 | |
| 13 | (0, 1, 2, 2, 3) | runcikantelirana 5 celica (runciprisekana 5 celica) |
60 | |
| 14 | (0, 1, 2, 3, 3) | dvojno kantiprisekana 5 celica (kantiprisekana 5 celica) |
60 | |
| 15 | (0, 1, 2, 3, 4) | omniprisekana 5 celica | 120 |
Skupina BC4
urediTa skupina ima diploidno heksadekahorično simetrijo reda 24*16=384: 4!=24 permutacij štirih osi, 24=16 pa je za zrcaljenje na vsaki osi.
Prisekanja teserakta
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) |
Slika oglišč |
Coxeter-Dinkinov in Schläflijevi simboli |
Število celic po položaju | Število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| položaj 3 (8) |
položaj
2 |
položaj 1 (32) |
položaj 0 (16) |
celice | stranske ploskve | robovi | oglišča | ||||
| 10 | 8 celica ali teserakt (tes) |

|
{4,3,3} |
(4) (4.4.4) |
8 | 24 | 32 | 16 | |||
| 11 | rektificirana 8 celica (rit) | 
|
t1{4,3,3} |
(3) (3.4.3.4) |
(2) (3.3.3) |
24 | 88 | 96 | 32 | ||
| 13 | prisekana 8 celica (tat) | 
|
t0,1{4,3,3} |
(3) (3.8.8) |
(1) (3.3.3) |
24 | 88 | 128 | 64 | ||
| 14 | kantelirana 8 celica (srit) | 
|
t0,2{4,3,3} |
(1) (3.4.4.4) |
(2) (3.4.4) |
(1) (3.3.3.3) |
56 | 248 | 288 | 96 | |
| 15 | runcinirana 8 celica (tudi runcinirana 16 celica) (sidpith) |

|
t0,3{4,3,3} |
(1) (4.4.4) |
(3) (4.4.4) |
(3) (3.4.4) |
(1) (3.3.3) |
80 | 208 | 192 | 64 |
| 16 | dvojno prisekana 8 celica (tudi dvojno prisekana 16 celica) (tah) |

|
t1,2{4,3,3} |
(2) (4.6.6) |
(2) (3.6.6) |
24 | 120 | 192 | 96 | ||
| 18 | kantiprisekana 8 celica (grit) | 
|
t0,1,2{4,3,3} |
(2) (4.6.8) |
(1) (3.4.4) |
(1) (3.6.6) |
56 | 248 | 384 | 192 | |
| 19 | runciprisekana 8 celica (proh) | t0,1,3{4,3,3} |
(1) (3.8.8) |
(2) (4.4.8) |
(1) (3.4.4) |
(1) (3.4.3.4) |
80 | 368 | 480 | 192 | |
| 21 | omniprisekana 8 celica (tudi omniprisekana 16 celica) (gidpith) |

|
t0,1,2,3{3,3,4} |
(1) (4.6.8) |
(1) (4.4.8) |
(1) (4.4.6) |
(1) (4.6.6) |
80 | 464 | 768 | 384 |
| 12 | polteserakt 16 celica (hex) |

|
h0{4,3,3} |
(3.3.3) |
(half) (3.3.3) |
16 | 32 | 24 | 8 | ||
Prisekanja 16 celice
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) | slika oglišč |
Coxeter-Dinkinov diagram in Schläflijevi simboli |
število celic po položaju | Število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| položaj 3 (8) |
položaj 2 (24) |
položaj 1 (32) |
položaj 0 (16) |
Celice | Stranske ploskve | Robovi | Oglišča | ||||
| [12] | 16 celica (hex) | 
|
{3,3,4} |
(8) (3.3.3) |
16 | 32 | 24 | 8 | |||
| [22] | *rektificirana 16 celica (isto kot 24 celica) (ico) |

|
t1{3,3,4} |
(2) (3.3.3.3) |
(4) (3.3.3.3) |
24 | 96 | 96 | 24 | ||
| 17 | prisekana 16 celica (thex) | 
|
t0,1{3,3,4} |
(1) (3.3.3.3) |
(4) (3.6.6) |
24 | 96 | 120 | 48 | ||
| [23] | *kantelirana 16 celica (isto kot rektificirana 24 celica) (rico) |

|
t0,2{3,3,4} |
(1) (3.4.3.4) |
(2) (4.4.4) |
(2) (3.4.3.4) |
48 | 240 | 288 | 96 | |
| [15] | runcinirana 16 celica (tudi runcinirana 8 celica) (sidpith) |

|
t0,3{3,3,4} |
(1) (4.4.4) |
(3) (4.4.4) |
(3) (3.4.4) |
(1) (3.3.3) |
80 | 208 | 192 | 64 |
| [16] | dvojno prisekana 16 celica (tudi dvojno prisekana 8 celica) (tah) |

|
t1,2{3,3,4} |
(2) (4.6.6) |
(2) (3.6.6) |
24 | 120 | 192 | 96 | ||
| [24] | *kantiprisekana 16 celica (isto kot prisekana 24 celica) (tico) |

|
t0,1,2{3,3,4} |
(1) (4.6.6) |
(1) (4.4.4) |
(2) (4.6.6) |
48 | 240 | 384 | 192 | |
| 20 | runciprisekana 16 celica (prit) | t0,1,3{3,3,4} |
(1) (3.4.4.4) |
(1) (4.4.4) |
(2) (4.4.6) |
(1) (3.6.6) |
80 | 368 | 480 | 192 | |
| [21] | omniprisekana 16 celica (tudi omniprisekana 8 celica) (gidpith) |

|
t0,1,2,3{3,3,4} |
(1) (4.6.8) |
(1) (4.4.8) |
(1) (4.4.6) |
(1) (4.6.6) |
80 | 464 | 768 | 384 |
| [31] | alternirana kantiprisekana 16 celica (isto kot prirezana 24-celica) (sadi) |

|
h0,1,2{3,3,4} |
(1) (3.3.3.3.3) |
(1) (3.3.3) |
(4) (3.3.3) |
(2) (3.3.3.3.3) |
144 | 480 | 432 | 96 |
- (*) Tako kot rektifikacija tetraedra naredi oktaeder, tako tudi rektifikacija 16 celice naredi 24 celico, ki je član naslednje skupine (družine).
Prirezana 24-celica je običajno v tej skupini zaradi popolnosti. To je alternacija kantiprisekane16 celice ali prisekane 24 celice s polovično simetrijsko grupo [(3,3)+,4]. Prisekane oktaederske celice postanejo ikozaedri. Kocka postane tetraeder in 96 novih tetraedrov nastane v prazninah odstranjenih oglišč.
Grafi
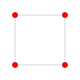
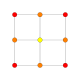
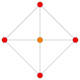
urediSlike so prikazane kot projekcije v perspektivi Schleglovih diagramov usrediščenih na celice v položaju 3 s primerno orientacijo in 16 celic na položaju 0, ki so prikazane z drugačno barvo.
| # | Johnsonovo
ime |
projekcije Coxeterjeva ravnina | Schleglovi diagrami | |||||
|---|---|---|---|---|---|---|---|---|
| F4 [12/3] |
B4 [8] |
B3 [6] |
B2 [4] |
A3 [4] |
kocka usrediščena |
tetraeder usrediščen | ||
| 10 | 8 celica ali teserakt (tes) |

|

|

|
|
|

|
|
| 11 | rektificirana 8 celica (rit) | 
|

|

|

|

|

|
|
| 12 | 16 celica (hex) | 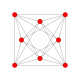
|

|

|
|
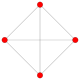
|

| |
| 13 | prisekana 8 celica (tat) | 
|

|
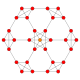
|
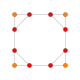
|
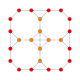
|

|
|
| 14 | kantelirana 8 celica (srit) | 
|

|

|
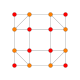
|
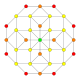
|

|
|
| 15 | runcinirana 8 celica (tudi runcinirana 16 celica) (sidpith) |

|

|
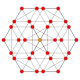
|

|

|

|

|
| 16 | dvojno prisekana 8 celica (tudi dvojno prisekana 16 celica) (tah) |

|

|

|

|

|

|

|
| 17 | prisekana 16 celica (thex) | 
|

|

|

|
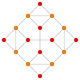
|

| |
| 18 | kantiprisekana 8 celica (grit) | 
|

|
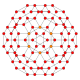
|
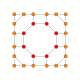
|
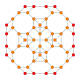
|

|
|
| 19 | runciprisekana 8 celica (proh) | 
|

|

|
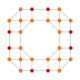
|

|

|
|
| 20 | runciprisekana 16 celica (prit) | 
|

|
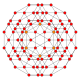
|

|
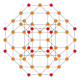
|

| |
| 21 | omniprisekana 8 celica (tudi omniprisekana 16 celica) (gidpith) |

|

|

|
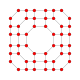
|
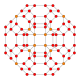
|

|

|
| [22] | *rektificirana 16 celica (isto kot 24 celica) (ico) |

|

|

|
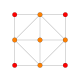
|

|

| |
| [23] | *kantelirana 16 celica (isto kot rektificirana 24 celica) (rico) |

|

|

|

|

|

| |
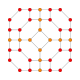
| [24] | *kantiprisekana 16 celica (isto kot prisekana 24 celica) (tico) |

|

|

|
|

|

| |
| [31] | alternirana kantiprisekana 16 celica (isto kot prirezana 24-celica) (sadi) |

|

|

|

|

| ||
Koordinate
urediTeseraktna skupina polihoronov je podana s pomočjo konveksnih ogrinjač z določenimi osnovnimi točkami, ki so naštete v naslednji tabeli z vsemi permutacijami koordinat. Vsak osnovna točka generira drugi uniformni polihoron. Vse koordinate pripadajo uniformnemu polihoronu, ki ima dolžino roba enako 2.
| # | Osnovna točka | Johnsonovo ime Bowersovo ime (okrajšava na Bowersov način) |
Coxeter-Dinkin |
|---|---|---|---|
| 1 | (0,0,0,1)√2 | 16 celica heksadekahoron (hex) |
|
| 2 | (0,0,1,1)√2 | rektificirana 16 celica ikozitetrahoron (ico) |
|
| 3 | (0,0,1,2)√2 | prisekana 16 celica prisekani heksadekahoron (thex) |
|
| 4 | (0,1,1,1)√2 | rektificiran teserakt (dvojno rektificirana 16 celica) rektificirani teserakt (rit) |
|
| 5 | (0,1,1,2)√2 | kantelirana 16 celica rektificirani ikozitetrahoron (rico) |
|
| 6 | (0,1,2,2)√2 | dvojno prisekana 16 celica teseraktiheksadekahoron (tah) |
|
| 7 | (0,1,2,3)√2 | kantiprisekana 16 celica prisekani ikozotetrahoron (tico) |
|
| 8 | (1,1,1,1) | teserakt teserakt (tes) |
|
| 9 | (1,1,1,1) + (0,0,0,1)√2 | runcinirani teserakt (runcinirana 16 celica) mali diprizmoteseraktiheksadekahoron (sidpith) |
|
| 10 | (1,1,1,1) + (0,0,1,1)√2 | kantelirani teserakt mali rombski teserakt (srit) |
|
| 11 | (1,1,1,1) + (0,0,1,2)√2 | runcinirana 16 celica prizmatorombski teserakt (prit) |
|
| 12 | (1,1,1,1) + (0,1,1,1)√2 | prisekani teserakt prisekani teserakt (tat) |
|
| 13 | (1,1,1,1) + (0,1,1,2)√2 | runciprisekani teserakt (runcikantelirana 16 celica) prizmatorombski heksadekahoron (proh) |
|
| 14 | (1,1,1,1) + (0,1,2,2)√2 | kantiprisekani teserakt veliki rombski teserakt (grit) |
|
| 15 | (1,1,1,1) + (0,1,2,3)√2 | omniprisekana 16 celica (omniprisekani teserakt) veliki disprizmatoteseraktiheksadekahoron (gidpith) |
Skupina F4
urediTa skupina ima diploidno ikozitetrahorsko simetrijo reda 24*48=1152: 48 simetrij oktaedra za vsakih 24 celic.
| # | Ime | Slika oglišč |
Coxeter-Dinkinov in Schläflijevi simboli |
Število celic po položaju | Število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| položaj 3 (24) |
položaj 2 (96) |
položaj 1 (96) |
položaj 0 (24) |
Celice | Stranske ploskve | Robovi | Oglišča | ||||
| 22 | 24 celica (isto kot rektificirana 16 celica) (ico) |

|
{3,4,3} |
(6) (3.3.3.3) |
24 | 96 | 96 | 24 | |||
| 23 | rektificirana 24 celica (isto kot kantelirana 16 celica) (rico) |

|
t1{3,4,3} |
(3) (3.4.3.4) |
(2) (4.4.4) |
48 | 240 | 288 | 96 | ||
| 24 | prisekana 24 celica (isto kot kantiprisekana 16 celica) (tico) |

|
t0,1{3,4,3} |
(3) (4.6.6) |
(1) (4.4.4) |
48 | 240 | 384 | 192 | ||
| 25 | kantelirana 24 celica (srico) | 
|
t0,2{3,4,3} |
(2) (3.4.4.4) |
(2) (3.4.4) |
(1) (3.4.3.4) |
144 | 720 | 864 | 288 | |
| 26 | *runcinirana 24 celica (spic) | 
|
t0,3{3,4,3} |
(1) (3.3.3.3) |
(3) (3.4.4) |
(3) (3.4.4) |
(1) (3.3.3.3) |
240 | 672 | 576 | 144 |
| 27 | *dvojno prisekana 24 celica (cont) | 
|
t1,2{3,4,3} |
(2) (3.8.8) |
(2) (3.8.8) |
48 | 336 | 576 | 288 | ||
| 28 | kantiprisekana 24 celica (grico) | 
|
t0,1,2{3,4,3} |
(2) (4.6.8) |
(1) (3.4.4) |
(1) (3.8.8) |
144 | 720 | 1152 | 576 | |
| 29 | runciprisekana 24 celica (prico) | t0,1,3{3,4,3} |
(1) (4.6.6) |
(2) (4.4.6) |
(1) (3.4.4) |
(1) (3.4.4.4) |
240 | 1104 | 1440 | 576 | |
| 30 | *omniprisekana 24 celica (gippic) | 
|
t0,1,2,3{3,4,3} |
(1) (4.6.8) |
(1) (4.4.6) |
(1) (4.4.6) |
(1) (4.6.8) |
240 | 1392 | 2304 | 1152 |
| 31 | alternirana prisekana 24 celica †(isto kot prirezana 24-celica) (sadi) |

|
h0,1{3,4,3} |
(3) (3.3.3.3.3) |
(4) (3.3.3) |
(1) (3.3.3) |
144 | 480 | 432 | 96 | |
- (*) Tako kot je 5 celica sebi dualna je tudi 24 celica sebi dualna in tako imajo tri imena, označena z zvezdico, dvakrat toliko simetrij. To pa da skupaj 2304 (razširjana ikozitetrahorna grupa [[3,4,3]]).
- (†) Prirezana 24-celica kljub imenu ni analog prirezani kocki, ker se dobi z alternacijo iz prisekane 24 celice. Njena številka simetrije je 576, (ionsko zmanjšana ikozitetrahorna grupa, [3+,4,3]).
Grafi
uredi| # | Name Coxeter-Dinkinov Schläflijev simbol |
Graf |
Schleglov diagram |
Ortogonalna projekcija | ||||
|---|---|---|---|---|---|---|---|---|
| F4 [12] |
B4 [8] |
B3 [6] |
B2 [4] |
oktaeder usrediščen |
dualni oktaeder usrediščen |
oktaeder usrediščen | ||
| 22 | 24 celica (ico) (rektificirana 16 celica) {3,4,3} |

|

|

|

|

| ||
| 23 | rektificirana 24 celica (rico) (kantelirana 16 celica) t1{3,4,3} |

|

|

|

|

| ||
| 24 | prisekana 24 celica (tico) (kantiprisekana 16 celica) t0,1{3,4,3} |

|

|

|

|

| ||
| 25 | kantelirana 24 celica (srico) t0,2{3,4,3} |

|

|

|

|

| ||
| 26 | *runcinirana 24 celica (spic) t0,3{3,4,3} |

|

|

|

|

| ||
| 27 | *dvojno prisekana 24 celica (cont) t1,2{3,4,3} |

|

|

|

|

| ||
| 28 | kantiprisekana 24 celica (grico) t0,1,2{3,4,3} |

|

|

|

|

| ||
| 29 | runciprisekana 24 celica (prico) t0,1,3{3,4,3} |

|

|

|

|

| ||
| 30 | *omniprisekana 24 celica (gippic) t0,1,2,3{3,4,3} |

|

|

|

|

| ||
| 31 | alternirana prisekana 24 celica †(isto kot prirezana 24-celica) (sadi) h0,1{3,4,3} |

|

|

|

|

|

| |
Koordinate
urediKoordinate oglišč za vseh 15 oblik je podanih v nadaljevanju, vključno z dualno obliko dveh pravilnih 24 celic. (dualne oblike so prikazane v mastnem tisku.) Aktivni kolobarji v prvem in drugem vozlu generirajo točke, ki so v prvem stolpcu. Aktivni kolobarji v tretjem in četrtem vozlu generirajo točke v drugem stolpcu. Vsota vsake izmed teh točk so permutirane po položaju koordinat in znaku kombinacij. To generira vse koordinate oglišč. Dolžina robov je enaka 2.
Edina izjema je prirezana 24-celica, ki je generirana s polovico permutacij koordinat, samo parno število koordinat se izmenjuje. φ=(√5+1)/2.
| Osnovne točke t(0,1) |
Osnovne točke t(2,3) |
Schläflijev simbol | Ime |
Coxeter-Dinkinov diagram |
|---|---|---|---|---|
| (0,0,1,1)√2 | t0{3,4,3} | 24 celica | ||
| (0,1,1,2)√2 | t1{3,4,3} | rektificirana 24 celica | ||
| (0,1,2,3)√2 | t0,1{3,4,3} | prisekana 24 celica | ||
| (0,1,φ,φ+1)√2 | h0,1{3,4,3} | prirezana 24-celica | ||
| (0,2,2,2) (1,1,1,3) |
t2{3,4,3} | Birectified 24-cell (rektificirana 24 celica) |
||
| (0,2,2,2) + (1,1,1,3) + |
(0,0,1,1)√2 " |
t0,2{3,4,3} | kantelirana 24 celica | |
| (0,2,2,2) + (1,1,1,3) + |
(0,1,1,2)√2 " |
t1,2{3,4,3} | dvojno prisekana 24 celica | |
| (0,2,2,2) + (1,1,1,3) + |
(0,1,2,3)√2 " |
t0,1,2{3,4,3} | kantiprisekana 24 celica | |
| (0,0,0,2) (1,1,1,1) |
t3{3,4,3} | trojno rektificirana 24 celica (24 celica) |
||
| (0,0,0,2) + (1,1,1,1) + |
(0,0,1,1)√2 " |
t0,3{3,4,3} | runcinirana 24 celica | |
| (0,0,0,2) + (1,1,1,1) + |
(0,1,1,2)√2 " |
t1,3{3,4,3} | dvojno kantelirana 24 celica (kantelirana 24 celica) |
|
| (0,0,0,2) + (1,1,1,1) + |
(0,1,2,3)√2 " |
t0,1,3{3,4,3} | runciprisekana 24 celica | |
| (1,1,1,5) (1,3,3,3) (2,2,2,4) |
t2,3{3,4,3} | trojno prisekana 24 celica (prisekana 24 celica) |
||
| (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + |
(0,0,1,1)√2 " " |
t0,2,3{3,4,3} | runciprisekana 24 celica (runciprisekana 24 celica) |
|
| (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + |
(0,1,1,2)√2 " " |
t1,2,3{3,4,3} | dvojno kantiprisekana 24 celica (kantiprisekana 24 celica) |
|
| (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + |
(0,1,2,3)√2 " " |
t0,1,2,3{3,4,3} | omniprisekana 24 celica | |
Skupina H4
urediTa skupina ima diploidno heksakozihorično simetrijo reda 120*120=24*600=14400: 120 je za vsakega od 120 dodekaedrov ali 24 za vsakega od 600 tetraedrov.
Prisekanja 120-celice
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) |
Slika oglišč |
Coxeter-Dinkin in Schläflijevi simboli |
Število celic po položaju | Število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| položaj 3 (120) |
položaj 2 (720) |
položaj 1 (1200) |
položaj 0 (600) |
Celice | Stranske ploskve | Robovi | Oglišča | ||||
| 32 | 120 celica (hi) | 
|
{5,3,3} |
(4) (5.5.5) |
120 | 720 | 1200 | 600 | |||
| 33 | rektificirana 120 celica (rahi) | 
|
t1{5,3,3} |
(3) (3.5.3.5) |
(2) (3.3.3) |
720 | 3120 | 3600 | 1200 | ||
| 36 | prisekana 120 celica (thi) | 
|
t0,1{5,3,3} |
(3) (3.10.10) |
(1) (3.3.3) |
720 | 3120 | 4800 | 2400 | ||
| 37 | kantelirana 120 celica (srahi) | 
|
t0,2{5,3,3} |
(1) (3.4.5.4) |
(2) (3.4.4) |
(1) (3.3.3.3) |
1920 | 9120 | 10800 | 3600 | |
| 38 | runcinirana 120 celica (tudi runcinirana 600 celica) (sidpixhi) |

|
t0,3{5,3,3} |
(1) (5.5.5) |
(3) (4.4.5) |
(3) (3.4.4) |
(1) (3.3.3) |
2640 | 7440 | 7200 | 2400 |
| 39 | dvojno prisekana 120 celica (tudi dvojno prisekana 600 celica) (xhi) |

|
t1,2{5,3,3} |
(2) (5.6.6) |
(2) (3.6.6) |
720 | 4320 | 7200 | 3600 | ||
| 42 | kantiprisekana 120 celica (grahi) | 
|
t0,1,2{5,3,3} |
(2) (4.6.10) |
(1) (3.4.4) |
(1) (3.6.6) |
1920 | 9120 | 14400 | 7200 | |
| 43 | runciprisekana 120 celica (prix) | t0,1,3{5,3,3} |
(1) (3.10.10) |
(2) (4.4.10) |
(1) (3.4.4) |
(1) (3.4.3.4) |
2640 | 13440 | 18000 | 7200 | |
| 46 | omniprisekana 120 celica (tudi omniprisekana 600 celica) (gidpixhi) |

|
t0,1,2,3{5,3,3} |
(1) (4.6.10) |
(1) (4.4.10) |
(1) |
(1) (4.6.6) |
2640 | 17040 | 28800 | 14400 |
Prisekanja 600 celice
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) |
slika oglišč |
Coxeter-Dinkinov in Schläflijevi simboli |
Število celic po položaju | Število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| položaj 3 (120) |
položaj 2 (720) |
položaj 1 (1200) |
položaj 0 (600) |
Celice | Stranske ploskve | Robovi | Oglišča | ||||
| 35 | 600 celica (ex) | 
|
{3,3,5} |
(20) (3.3.3) |
600 | 1200 | 720 | 120 | |||
| 34 | rektificirana 600 celica (rox) | 
|
t1{3,3,5} |
(2) (3.3.3.3.3) |
(5) (3.3.3.3) |
720 | 3600 | 3600 | 720 | ||
| 41 | prisekana 600 celica (tex) | 
|
t0,1{3,3,5} |
(1) (3.3.3.3.3) |
(5) (3.6.6) |
720 | 3600 | 4320 | 1440 | ||
| 40 | kantelirana 600 celica (srix) | 
|
t0,2{3,3,5} |
(1) (3.5.3.5) |
(2) (4.4.5) |
(1) (3.4.3.4) |
1440 | 8640 | 10800 | 3600 | |
| [38] | runcinirana 600 celica (tudi runcinirana 120 celica) (sidpixhi) |

|
t0,3{3,3,5} |
(1) (5.5.5) |
(3) (4.4.5) |
(3) (3.4.4) |
(1) (3.3.3) |
2640 | 7440 | 7200 | 2400 |
| [39] | dvojno prisekana 600 celica (tudi dvojno prisekana 120 celica) (xhi) |

|
t1,2{3,3,5} |
(2) (5.6.6) |
(2) (3.6.6) |
720 | 4320 | 7200 | 3600 | ||
| 45 | kantiprisekana 600 celica (grix) | 
|
t0,1,2{3,3,5} |
(1) (5.6.6) |
(1) (4.4.5) |
(2) (4.6.6) |
1440 | 8640 | 14400 | 7200 | |
| 44 | runciprisekana 600 celica (prahi) | t0,1,3{3,3,5} |
(1) (3.4.5.4) |
(1) (4.4.5) |
(2) (4.4.6) |
(1) (3.6.6) |
2640 | 13440 | 18000 | 7200 | |
| [46] | omniprisekana 600 celica (tudi omniprisekana 120 celica) (gidpixhi) |

|
t0,1,2,3{3,3,5} |
(1) (4.6.10) |
(1) (4.4.10) |
(1) (4.4.6) |
(1) (4.6.6) |
2640 | 17040 | 28800 | 14400 |
Grafi
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) |
projekcije na Coxeterjevo ravnino | Schleglovi diagrami | ||||||
|---|---|---|---|---|---|---|---|---|---|
| F4 [12] |
[20] | H4 [30] |
H3 [10] |
A3 [4] |
A2 [3] |
Dodekaeder usrediščen |
Tetraeder usrediščen | ||
| 32 | 120 celica (hi) |  |
 |
 |
 |
 |

|

|
|
| 33 | rektificirana 120 celica (rahi) |  |
 |
 |
 |
 |

|

|
|
| 34 | rektificirana 600 celica (rox) |  |
 |
 |
 |
 |

|

|
|
| 35 | 600 celica (ex) |  |
 |
 |
 |
 |

|

|

|
| 36 | prisekana 120 celica (thi) |  |
 |
 |
 |
 |

|

|
|
| 37 | kantelirana 120 celica (srahi) |  |

|

|
|||||
| 38 | runcinirana 120 celica (tudi runcinirana 600 celica) (sidpixhi) |
 |

|

|
|||||
| 39 | dvojno prisekana 120 celica (tudi dvojno prisekana 600 celica) (xhi) |
 |
 |

|

|
||||
| 40 | kantelirana 600 celica (srix) |  |
 |
 |
 |
 |

|

| |
| 41 | prisekana 600 celica (tex) |  |
 |
 |
 |
 |

|

| |
| 42 | kantiprisekana 120 celica (grahi) |  |

|

|
|||||
| 43 | runciprisekana 120 celica (prix) |  |

|

|
|||||
| 44 | runciprisekana 600 celica (prahi) |  |

|

| |||||
| 45 | kantiprisekana 600 celica (grix) |  |

|

| |||||
| 46 | omniprisekana 120 celica (tudi omniprisekana 600 celica) (gidpixhi) |
 |

|

|
|||||
Skupina D4
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) | slika oglišč |
Coxeter-Dinkinov diagram |
Število celic po položaju | Število elementov | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| položaj 0 (8) |
položaj 1 (24) |
položaj 2 (8) |
položaj 3 (8) |
položaj alt (96) |
3 | 2 | 1 | 0 | ||||
| [12] | polteserakt (isto kot 16 celica) (hex) |

|
t0{31,1,1} |
(4) (3.3.3) |
(4) (3.3.3) |
16 | 32 | 24 | 8 | |||
| [17] | prisekani polteserakt (isto kot prisekana 16 celica) (thex) |

|
t0,1{31,1,1} |
(1) (3.3.3.3) |
(2) (3.6.6) |
(2) (3.6.6) |
24 | 96 | 120 | 48 | ||
| [11] | kantelirani polteserakt (isto kot rektificirani teserakt) (rit) |

|
t0,2{31,1,1} |
(1) (3.3.3) |
(1) (3.3.3) |
(3) (3.4.3.4) |
24 | 88 | 96 | 32 | ||
| [16] | kantiprisekani polteserakt (isto kot dvojno prisekani teserakt) (tah) |

|
t0,1,2{31,1,1} |
(1) (3.6.6) |
(1) (3.6.6) |
(2) (4.6.6) |
24 | 96 | 96 | 24 | ||
| [22] | rektificirani polteserakt (isto kot rektificirana 16 celica) (isto kot 24 celica) (ico) |

|
t1{31,1,1} |
(2) (3.3.3.3) |
(2) (3.3.3.3) |
(2) (3.3.3.3) |
48 | 240 | 288 | 96 | ||
| [23] | runcikantelirani polteserakt (isto kot kantelirana 16 celica) (isto kot rektificirana 24 celica) (rico) |

|
t0,2,3{31,1,1} |
(1) (3.4.3.4) |
(2) (4.4.4) |
(1) (3.4.3.4) |
(1) (3.4.3.4) |
24 | 120 | 192 | 96 | |
| [24] | omniprisekani polteserakt (isto kot kantiprisekana 16 celica) (isto kot prisekana 24 celica) (tico) |

|
t0,1,2,3{31,1,1} |
(1) (4.6.6) |
(1) (4.4.4) |
(1) (4.6.6) |
(1) (4.6.6) |
48 | 240 | 384 | 192 | |
| [31] | snub polteserakt (isto kot prirezana 24-celica) (sadi) |

|
s{31,1,1} |
(1) (3.3.3.3.3) |
(1) (3.3.3) |
(1) (3.3.3.3.3) |
(1) (3.3.3.3.3) |
(4) (3.3.3) |
144 | 480 | 432 | 96 |
Grafi
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) Coxeter-Dinkinov diagram |
projekcije na Coxeterjevo ravnino | Schleglovi diagrami | vzporedni trirazsežni | |||
|---|---|---|---|---|---|---|---|
| B4 [8/2] |
D4 [6] |
D3 [2] |
kocka usrediščena |
tetraeder usrediščen |
D4 [6] | ||
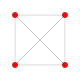
| [12] | polteserakt (isto kot 16 celica) (hex) t0{31,1,1} |

|

|
|

| ||
| [17] | prisekani polteserakt (isto kot prisekana 16 celica) (thex) t0,1{31,1,1} |

|

|

|

| ||
| [11] | kantelirani polteserakt (isto kot rektificirani teserakt) (rit) t0,2{31,1,1} |

|

|

|

|
||
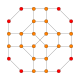
| [16] | kantiprisekani polteserakt (isto kot dvojno prisekani teserakt) (tah) t0,1,2{31,1,1} |

|

|
|

| ||
| [22] | rektificirani polteserakt (isto kot rektificirana 16 celica) (isto kot 24 celica) (ico) t1{31,1,1} |

|

|
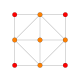
|

| ||
| [23] | runcikantelirani polteserakt (isto kot kantelirana 16 celica) (isto kot rektificirana 24 celica) (rico) t0,2,3{31,1,1} |

|

|

|

| ||
| [24] | omniprisekani polteserakt (isto kot kantiprisekana 16 celica) (isto kot prisekana 24 celica) (tico) t0,1,2,3{31,1,1} |

|

|

|

| ||
| [31] | prirezani polteserakt (prirezana 24-celica) (sadi) s{31,1,1} |

|

|

|

| ||
Koordinate
urediOsnovna točka lahko generira koordinate politopa tako, da se vzame vse permutacije koordinat in kombinacij predznakov. Dolžina robov bo tako √2. Nekateri politopi imajo po dve možni točki generiranja. Tem točkam lahko dodamo predpono parne, kar naj kaže, da štejemo samo permutacije s parnim predznakom.
| # | Osnovna točka | Johnsonovo in Bowersovo ime | Coxeter-Dinkinov diagram | Sorodni B4 Coxeter-Dinkinov diagram |
Sorodni F4 Coxeter-Dinkinov diagram |
|---|---|---|---|---|---|
| [12] | (0,0,0,2) | 16 celica | |||
| [22] | (0,0,2,2) | rektificirana 16 celica | |||
| [17] | (0,0,2,4) | prisekana 16 celica | |||
| [11] | (0,2,2,2) | kantelirana 16 celica | |||
| [23] | (0,2,2,4) | kantelirana 16 celica | |||
| [16] | (0,2,4,4) | dvojno prisekana 16 celica | |||
| [24] | (0,2,4,6) | kantiprisekana 16 celica | |||
| [31] | (0,1,φ,φ+1)/√2 | prirezana 24-celica | |||
| [12] | parna (1,1,1,1) | polteserakt (16 celica) |
|||
| [11] | parna (1,1,1,3) | kantelirani polteserakt (kantelirana 16 celica) |
|||
| [17] | parna (1,1,3,3) | prisekan polteserakt (prisekana 16 celica) |
|||
| [16] | parna (1,3,3,3) | kantiprisekan polteserakt (kantiprisekana 16 celica) |
Velika antiprizma
urediObstaja eden newythoffianov uniformni konveksni polihoron, ki je znan kot velika antiprizma. Ta je sestavljena iz 20 petstranih antiprizem. Te tvorijo dva pravokotna obroča, ki sta povezana s 300 tetraedri. Ta je analogna trirazsežni antiprizmam, ki so sestavljene iz dveh vzporednih mnogokotnikov, povezanih s pasom trikotnikov. V nasprotju z njimi velika antiprizma ne spada v neskončno skupino uniformnih politopov. Njihovo simetrijsko število je 400 (ionsko zmanjšana Coxeterjeva grupa).
| # | Johnsonovo ime (okrajšava na Bowersov način) | Slika | Slika oglišč |
Coxeter-Dinkinov diagram in Schläflijevi simboli |
celice po vrsti | Število elementov | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Celice | Stranske ploskve | Robovi | Oglišča | |||||||
| 47 | velika antiprizma (gap) | 
|
ni simbola | 300 (3.3.3) |
20 (3.3.3.5) |
320 | 20 {5} 700 {3} |
500 | 100 | |
Prizmatični uniformni polihoroni
urediPrizmatični politop je kartezični produkt dveh politopov z nižjo razsežnostjo. Znani primeri so trirazsežne prizme, ki so produkt mnogokotnika in daljice. Prizmatične uniformne polihorone sestavljata dve neskončni skupini:
- poliederske prizme: produkt daljice in uniformnega poliedra. Ta skupina je neskončna, ker vsebuje trirazsežne prizme in antiprizme.
- duoprizme: produkt dveh mnogokotnikov.
Konveksne poliederske prizme
urediNajbolj razumljiva družina prizmatičnih polihoronov so poliederske prizmeki so produkt poliedra z daljico. Celice takšnega polihorona sta dva identična uniformna poliedra, ki ležita v vzporednih ravninah (imenujemo jih osnovne celice) povezuje ju plast prizem (to so stranske celice). Ta družina vključuje prizme 75 neprizmatičnih uniformnih poliedrov.
Znanih je 18 konveksnih poliederskih prizem, ki jih naredimo iz 5 platonskih teles in 13 arhimedskih teles ter neskončno družino trirazsežnih prizem in antiprizem. Simetrijsko število poliedrskih prizem je dvakrat večje kot za osnovne poliedre.
Tetraederske prizme: A3 × A1
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) | Slika | Coxeter-Dinkinov diagram in Schläflijevi simboli |
Celice po vrsti | Število elementov | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Celice | Stranske ploskve | Robovi | Oglišča | |||||||
| 48 | tetraederska prizma (tepe) | 
|
t0{3,3}×{} |
2 3.3.3 |
4 3.4.4 |
6 | 8 {3} 6 {4} |
16 | 8 | |
| 49 | prisekana tetraederska prizma (tuttip) | 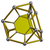
|
t0,1{3,3}×{} |
2 3.6.6 |
4 3.4.4 |
4 4.4.6 |
10 | 8 {3} 18 {4} 8 {6} |
48 | 24 |
| [51] | rektificirana tetraederska prizma (isto kot oktaederska prizma) (ope) |

|
t1{3,3}×{} |
2 3.3.3.3 |
4 3.4.4 |
6 | 16 {3} 12 {4} |
30 | 12 | |
| [50] | kantelirana tetraederska prizma (isto kot kubootaederska prizma) (cope) |

|
t0,2{3,3}×{} |
2 3.4.3.4 |
8 3.4.4 |
6 4.4.4 |
16 | 16 {3} 36 {4} |
60 | 24 |
| [54] | kantiprisekana tetraedrska prizma (isto kot prisekana oktaederska prizma) (tope) |

|
t0,1,2{3,3}×{} |
2 4.6.6 |
8 6.4.4 |
6 4.4.4 |
16 | 48 {4} 16 {6} |
96 | 48 |
| [59] | Prirezana tetraederska prizma (isto kot ikozaederska prizma) (ipe) |

|
s{3,3}×{} |
2 3.3.3.3.3 |
20 3.4.4 |
22 | 40 {3} 30 {4} |
72 | 24 | |
Oktaedrske prizme: BC3 × A1
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) | Slika | Coxeter-Dinkinov diagram in Schläflijevi simboli |
Celice po vrsti | število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Celice | Stranske ploskve | Robovi | Oglišča | ||||||||
| [10] | kubična prizma (isto kot teserakt) (isto kot 4-4 duoprizma) (tes) |

|
t0{4,3}×{} |
2 4.4.4 |
6 4.4.4 |
8 | 24 {4} | 32 | 16 | ||
| 50 | kubooktaedrska prizma (isto kot kantelirana tetraedrska prizma) (cope) |

|
t1{4,3}×{} |
2 3.4.3.4 |
8 3.4.4 |
6 4.4.4 |
16 | 16 {3} 36 {4} |
60 | 24 | |
| 51 | oktaederska prizma (isto kot rektificirana tetraedrska prizma) (isto kot tristrana antiprizmatična prizma) (ope) |

|
t2{4,3}×{} |
2 3.3.3.3 |
8 3.4.4 |
10 | 16 {3} 12 {4} |
30 | 12 | ||
| 52 | rombikubooktaederska prizma (sircope) | 
|
t0,2{4,3}×{} |
2 3.4.4.4 |
8 3.4.4 |
18 4.4.4 |
28 | 16 {3} 84 {4} |
120 | 96 | |
| 53 | prisekana kubična prizma (ticcup) | 
|
t0,1{4,3}×{} |
2 3.8.8 |
8 3.4.4 |
6 4.4.8 |
16 | 16 {3} 36 {4} 12 {8} |
96 | 48 | |
| 54 | prisekana oktaederska prizma (isto kot kantiprisekana tetraederska prizma) (tope) |

|
t1,2{4,3}×{} |
2 4.6.6 |
6 4.4.4 |
8 4.4.6 |
16 | 48 {4} 16 {6} |
96 | 48 | |
| 55 | prisekana kubooktaederska prizma (gircope) | 
|
t0,1,2{4,3}×{} |
2 4.6.8 |
12 |
8 4.4.6 |
6 4.4.8 |
28 | 96 {4} 16 {6}<>12 {8} |
192 | 96 |
| 56 | prirezana kubična prizma (sniccup) | 
|
s{4,3}×{} |
2 3.3.3.3.4 |
32 3.4.4 |
6 4.4.4 |
40 | 64 {3} 72 {4} |
144 | 48 | |
Ikozaedrske prizme: H3 × A1
uredi| # | Johnsonovo ime (okrajšava na Bowersov način) | Slika | Coxeter-Dinkinov diagram in Schläflijevi simboli |
Celice po vrsti | Število elementov | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Celice | Stranske ploskve | Robovi | Oglišča | ||||||||
| 57 | dodekaederska prizma (dope) | 
|
t0{5,3}×{} |
2 5.5.5 |
12 4.4.5 |
14 | 30 {4} 24 {5} |
80 | 40 | ||
| 58 | ikozaederska prizma (iddip) | 
|
t1{5,3}×{} |
2 3.5.3.5 |
20 3.4.4 |
12 4.4.5 |
34 | 40 {3} 60 {4} 24 {5} |
150 | 60 | |
| 59 | ikozaederska prizma (isto kot prirezana tetraedrska prizma) (ipe) |

|
t2{5,3}×{} |
2 3.3.3.3.3 |
20 3.4.4 |
22 | 40 {3} 30 {4} |
72 | 24 | ||
| 60 | prisekana dodekaederska prizma (tiddip) | 
|
t0,1{5,3}×{} |
2 3.10.10 |
20 3.4.4 |
12 4.4.5 |
34 | 40 {3} 90 {4} 24 {10} |
240 | 120 | |
| 61 | rombiikozidodekaederska prizma (sriddip) | 
|
t0,2{5,3}×{} |
2 3.4.5.4 |
20 3.4.4 |
30 4.4.4 |
12 4.4.5 |
64 | 40 {3} 180 {4} 24 {5} |
300 | 120 |
| 62 | prisekana ikozaederska prizma (tipe) | 
|
t1,2{5,3}×{} |
2 5.6.6 |
12 4.4.5 |
20 4.4.6 |
34 | 90 {4} 24 {5} 40 {6} |
240 | 120 | |
| 63 | prisekana ikozaedrska prizma (griddip) | 
|
t0,1,2{5,3}×{} |
2 4.6.4.10 |
30 4.4.4 |
20 4.4.6 |
12 4.4.10 |
64 | 240 {4} 40 {6} 24 {5} |
480 | 240 |
| 64 | prirezana dodekaedrska prizma (sniddip) | 
|
s{5,3}×{} |
2 3.3.3.3.5 |
80 3.4.4 |
12 4.4.5 |
94 | 240 {4} 40 {6} 24 {10} |
360 | 120 | |
Duoprizme: [p] × [q]
uredi
Druga skupina je neskončna družina uniformnih duoprizem, ki so produkt dveh pravilnih mnogokotnikov.
Njihov Coxeter-Dinkinov diagram ima obliko ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ta družina se prekriva s prvim ko je eden izmed "faktorjev" mnogokotnikov kvadrat. Produkt je enak hiperprizmi katere osnovnica je trirazsežna prizma. Simetrijsko število duoprizme katere faktorja sta p-kotnik in q-kotnik (to da "p,q-duoprizmo") je 4pq kadar je p≠q; v primeru, da sta oba faktorja p-kotnika. Simetrijsko število je 8p2. Tudi teserakt lahko obravnavamo kot duoprizmo 4,4.
Elementi p,q-duoprizme (p ≥ 3, q ≥ 3) so:
- Celice: p q-stranskih prizem, q p-stranskih prizem
- Stranske ploskve: pq kvadrati, p q-kotniki, q p-kotniki
- Robovi: 2pq
- Oglišča: pq
Mnogokotne prizmatične prizme: [p] × [ ] × [ ]
urediNeskončna množica uniformnih prizmatičnih prizem se prekriva z 4-p duoprizmami: (p≥3) - ![]()
![]()
![]()
![]()
![]()
![]()
![]() - p cubes and 4 p-gonal prisms – (vse so enake kot 4-p duoprizme)
- p cubes and 4 p-gonal prisms – (vse so enake kot 4-p duoprizme)
| Ime | Coxeterjev graf | Celice |
|---|---|---|
| tristrana prizmatična prizma (tisdip) | 3 kocke in 4 tristrane prizme (isto kot 3-4 duoprizma) | |
| Square prismatic prism (tes) | 4 kocke in 4 kocke (isto kot 4-4 duoprizma in isto kot teserakt) | |
| petstrana prizmatična prizma (squipdip) | 5 kock in 4 petstranih prizem (isto kot 4-5 duoprizma) | |
| šeststrana prizmatična prizma (shiddip) | 6 kock in 4 šeststranih prizem (isto kot 4-6 duoprizma) | |
| sedemstrana prizmatična prizma (shedip) | 7 kock in 4 sedemstrane prizme (isto kot 4-7 duoprizma) | |
| osemstrana prizmatična prizma (sodip) | 8 kock in 4 osemstranih prizem (isto kot 4-8 duoprizma) |
Neskončna množica uniformih antiprizmatičnih prizem se lahko konstruira s pomočjo dveh vzporednih uniformnih antiprizem: (p≥3) - ![]()
![]()
![]()
![]()
![]()
![]()
![]() - 2 p-strane antiprizme povezane z 2 p-stranima prizmama in 2p tristranih prizem.
- 2 p-strane antiprizme povezane z 2 p-stranima prizmama in 2p tristranih prizem.
| Ime | Coxeterjev graf | Celice | Slika |
|---|---|---|---|
| tristrana antiprizmatična prizma (ope) | 2 oktaedra povezana z 8 tristranimi prizmami (isto kot oktaederska prizma) | ||
| kvadratna antiprizmatična prizma (squapip) | 2 kvadratni antiprizmi povezani z 2 kockama in 8 tristranimi prizmami | 
| |
| petstrana antiprizmatična prizma (pappip) | 2 petstrani antiprizmi povezani z 2 petstranima prizmama in 10 tristranimi prizmami | 
| |
| šeststrana antiprizmatična prizma (happip) | 2 šeststrani antiprizmi povezani z 2 šeststranima prizmama in 12 tristranimi prizmami | ||
| sedemstrana antiprizmatična prizma (heappip) | 2 sedemstrani antiprizmi povezani z 2 sedemstranima prizmama in 14 tristranih prizem | ||
| osemstrana antiprizmatična prizma (oappip) | 2 osemstrani antiprizmi povezani z 2 osemstranima prizmama in 16 tristranimi prizmami |
P-strana antiprizmatična prizma ima 4p trikotnike, 4p kvadratov in 4 p-kotne stranske ploskve. Ima 10p robov in 4p oglišč.
Neuniformne alternacije
urediZnanih je veliko alternacij uniformnega polihorona, ki se jih lahko obravnava kot uniformne, ker vsebujejo preveč parametrov, ki jim morajo zadoščati.
Za prirezana telesa niso uniforma za razliko od njihovih trirazsežnih analogov. samo prirezana 24-celica je uniformna, čeprav bi bilo boljše, če bi jo imenovali polprirezana 24-celica ali prirezani polteserakt, ker je polni snub družine D4 s polteseraktom kot alterniranim teseraktom.
- prirezana 5-celica (snip), s{3,3,3},






 , 10 ikozaedrov, 20 oktaedrov, in 60 tetraedri
, 10 ikozaedrov, 20 oktaedrov, in 60 tetraedri - prirezani teserakt (snit), s{4,3,3},






 , s 16 ikozaedrov, 32 oktaedrov, 24 kvadratnih antiprizem, 8 prirezanih kock in 192 tetraedrov
, s 16 ikozaedrov, 32 oktaedrov, 24 kvadratnih antiprizem, 8 prirezanih kock in 192 tetraedrov - polna prirezana 24-celica (snico), s{3,4,3},






 , from 48 prirezanih kock, 192 oktaedrov in 576 tetraedrov
, from 48 prirezanih kock, 192 oktaedrov in 576 tetraedrov - prirezana 120-celica (snahi), s{5,3,3},






 , 1200 oktaedrov, 600 ikozaedrov, 720 petstranih antiprizem, 120 prirezanih dodekaedrov in 7200 tetraedrov
, 1200 oktaedrov, 600 ikozaedrov, 720 petstranih antiprizem, 120 prirezanih dodekaedrov in 7200 tetraedrov
Poliederske prizme ![]()
![]()
![]()
![]()
![]()
![]()
![]() lahko alterniramo v
lahko alterniramo v ![]()
![]()
![]()
![]()
![]()
![]()
![]() , toda ne dajo uniformnih rešitev.
, toda ne dajo uniformnih rešitev.
- prirezana tetraedrska antiprizma, s{3,3,2}






 , 2 ikozaedra povezana s 6 tetraedri in 8 oktaedri s 24 tetraedri v izmenjujočih se luknjah.
, 2 ikozaedra povezana s 6 tetraedri in 8 oktaedri s 24 tetraedri v izmenjujočih se luknjah. - prirezana kubična antiprizma, s{4,3,2}






 , 2 prirezani kocki povezani z 12 tetraedri, 6 kvadratnimi antiprizmami in 8 oktaedri ter z 48 tetraedri v izmenjujočih se luknjah.
, 2 prirezani kocki povezani z 12 tetraedri, 6 kvadratnimi antiprizmami in 8 oktaedri ter z 48 tetraedri v izmenjujočih se luknjah. - prirezana dodekaedrska antiprizma, s{5,3,2}






 , 2 prirezana dodekaedra sta povezana s 30 tetraedri, 12 petstranih antiprizem in 20 oktaedrov s 120 tetraedri v izmenjajočih se luknjah.
, 2 prirezana dodekaedra sta povezana s 30 tetraedri, 12 petstranih antiprizem in 20 oktaedrov s 120 tetraedri v izmenjajočih se luknjah.
Duoprizme ![]()
![]()
![]()
![]()
![]()
![]()
![]() , t0,1,2,3{p,2,q} lahko alterniramo v
, t0,1,2,3{p,2,q} lahko alterniramo v ![]()
![]()
![]()
![]()
![]()
![]()
![]() , s{p,2,q}, ki se imenujejo duoantiprizme, ki v splošnem ne morajo postati uniformne. Edina konveksna uniformna rešitev je trivialni primer of p=q=2, which is a lower symmetry construction of the tesseract
, s{p,2,q}, ki se imenujejo duoantiprizme, ki v splošnem ne morajo postati uniformne. Edina konveksna uniformna rešitev je trivialni primer of p=q=2, which is a lower symmetry construction of the tesseract ![]()
![]()
![]()
![]()
![]()
![]()
![]() , t0,1,2,3{2,2,2}, ki je konstrukcija teserakta z alternacijo 16 celice,
, t0,1,2,3{2,2,2}, ki je konstrukcija teserakta z alternacijo 16 celice, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , s{2,2,2}.
, s{2,2,2}.
Geometrijska izpeljava za 46 neprizmatičnih uniformnih polihoronov
uredi
46 Wythoffovih polihoronov vključuje šest konveksni pravilni polihoron. Ostalih 40 se dobi iz pravilnih polihoronov z operacijo, ki ohranja večino njihovih simetrij. Tako jih lahko razvrstimo glede na njihove simetrijske grupe, ki jih imajo.
Geometrijske operacije, ki omogočajo dobiti 40 uniformnih polihoronov iz pravilnih polihoronov, je operacija prisekanja. Polihoron lahko prisekamona robovih, ogliščih ali stranskih ploskvah. To vodi k dodajanju celic, ki odgovarjajo tem elementom. To je prikazano tudi v spodnji preglednici.
Coxeter-Dinkinov diagram kaže štiri zrcala Wythoffovega kalejdoskopa kot vozle. Robovi med vozli so označeni s celimi števili in st tem kažejo kot med zrcali (π/n radianov ali 180/n stopinj). Obkroženi vozli kažejo katera zrcala so za določeno obliko aktivna. Zrcalo je aktivno glede na oglišče, ki ne leži na njem.
| Operacija | Schläflijev simbol |
Coxeter-Dinkinov diagram | Opis |
|---|---|---|---|
| Starševsko telo | t0{p,q,r} | Prvotna pravilna oblika {p,q,r} | |
| Rektifikacija | t1{p,q,r} | Operacija prisekanja se izvaja tako dolgo, da prvotni robovi degenerirajo v točko. | |
| Dvojna rektifikacija | t2{p,q,r} | Stranska ploskev se popolnoma priseka do točke. Isto kot rektificirani dual. | |
| Trojna rektifikacija (dual) |
t3{p,q,r} | Celice se prisekajo do točke. Pravilno dualno telo {r,q,p} | |
| Prisekanost | t0,1{p,q,r} | Vsako oglišče se odreže tako, da sredina prvotnega roba ostane. Kjer je oglišče se pojavi nova celica, ki je starševska slika oglišč. Tudi vsaka prvotna celica se enako prireže. | |
| Dvojno prisekanje | t1,2{p,q,r} | Prisekanje med rektificirano obliko in dualom rektificirane oblike. | |
| Trojno prisekanje | t2,3{p,q,r} | Prisekani dual {r,q,p}. | |
| Kantelacija | t0,2{p,q,r} | Prisekanje uporabljeno za robove in oglišča. Določa razvojno stopnjo med pravilno in dualno rektificirano obliko. | |
| Dvojna kantelacija | t1,3{p,q,r} | Kantelirani dual {r,q,p}. | |
| Runcinacija (ali razširitev) |
t0,3{p,q,r} | Prisekanje uporabljeno na celicah, stranskih ploskvah in robovih. Določa razvojno stopnjo med pravilno obliko in dualom. | |
| Kantiprisekanje | t0,1,2{p,q,r} | Skupna uporaba operacij kantelacija in prisekanje. | |
| Dvojno kantiprisekanje | t1,2,3{p,q,r} | Kantiprisekani dual {r,q,p}. | |
| Runciprisekanje | t0,1,3{p,q,r} | Uporaba dveh operacij runcinacije in prisekanja . | |
| Runcikatelacija | t0,1,3{p,q,r} | Runciprisekani dual {r,q,p}. | |
| Omniprisekanost (ali bolj določeno runcikantiprisekanost) |
t0,1,2,3{p,q,r} | Uporaba vseh treh operacij. | |
| prirezanost | s{p,q,r} | Alternacija omniprisekane oblike (obroči so zamenjani z luknjami). |
Sklici
uredi- ↑ T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- ↑ http://dissertations.ub.rug.nl/SlikaS/faculties/science/2007/i.polo.blanco/c5.pdf
- ↑ 2004 Dissertation: VierdimensionaleArhimedishe Polytope Arhivirano 2005-03-22 na Wayback Machine. (nemško)
- ↑ http://googology.wikia.com/wiki/Jonathan_Bowers
Zunanje povezave
uredi- Weisstein, Eric Wolfgang. »Uniform Polychoron«. MathWorld.
- konveksni uniformni polihoroni
- Uniformni politopi v štirih razsežnostih (angleško)
- Konveksni uniformni polihoroni osnovani na pentahoronu (5-celica) (angleško)
- Konveksni uniformni polihoroni osnovani na teseraktu (8 celica) in heksadekakronu (16 celica) (angleško)
- Konveksni uniformni polihoroni osnovani na ikozitetrahoronu (24 celica) (angleško)
- Konveksni uniformni polihoroni osnovani na hekatoniikozahoronu (120 celica) in heksakozihoronu (600 celica) (angleško)
- Nenormalni konveksni uniformni polihoron
- Konveksni uniformni prizmatični polihoroni (angleško)
- Uniformni polihoroni dobljeni iz glomeričnih tetraedrov B4 (angleško)
- Java apleti Arhivirano 2011-07-18 na Wayback Machine. (angleško)