Prisekani kubooktaeder
| Prisekani kubooktaeder | |
|---|---|
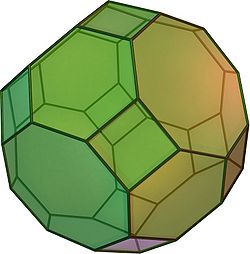 (animacija) | |
| vrsta | arhimedsko telo uniformni polieder |
| elementi | F = 26, E = 72, V = 4 8 (χ = 2) |
| stranske ploskve na stran | 12{4} + 8{6} + 6{8} |
| Conwayjev zapis | bC ali taC |
| Schläflijevi simboli | tr{4,3} ali |
| t0,1,2{4,3} | |
| Wythoffov simbol | 2 3 4 | |
| Coxeter-Dinkinov diagram | |
| simetrija | Oh, B3, [4,3], (*432), red 48 |
| vrtilna grupa | O, [4,3]+, (432), red 24 |
| diedrski kot | 4-6: arccos(-√6/3 = 144º 44′ 08″ 4-8: arccos(-√2/3) = 135º 6-8: arccos(-√3/3) = 125º 15′ 51″ |
| sklici | U11, C23, W15 |
| značilnosti | konveksen polpravilen zonoeder |
 obarvane stranske ploskve |
 4.6.8 (slika oglišč) |
 disdiakisni dodekaeder disdiakisni dodekaeder (dualni polieder) |
 mreža telesa |
Prisekani kubooktaeder je v geometriji konveksni polieder. Je arhimedsko telo, eno od trinajstih konveksnih izogonalnih neprizmatičnih teles skonstruirano z dvema ali več vrstami pravilnih mnogokotniških stranskih ploskev.
Ima šestindvajset pravilnih stranskih ploskev, od tega dvanajst kvadratnih, osem šestkotniških in šest osemkotniških, ter 72 robov in 48 oglišč. Ker ima vsaka stranska ploskev točkovno simetrijo, kar je enakovredno vrtilni simetriji, je to telo tudi zonoeder.
Druga imena
urediIzmenoma se uporabljajo tudi drugačna imena za prisekani kubooktaeder:
Ime prisekani kubooktaeder je dal telesu nemški astrolog, astronom in matematik Johannes Kepler (1571–1630). To ime je malo zavajoče. Če se priseka kubooktaeder tako, da se odstrani oglišča, se ne dobi takšnega uniformnega telesa. Nekatere stranske ploskve bi bile pravokotniki. Rezultirajoče telo je topološko enakovredno prisekanemu kubooktaedru, ki se ga vedno lahko spremeni, dokler so stranske ploskve pravilne.
Drugo ime "veliki rombikubooktaeder" se nanaša na dejstvo, da 12 kvadratnih stranskih ploskev leži v istih ravninah kot stranske ploskve rombskega dodekaedra, 6 osemkotnih v istih ravninah kot stranske ploskve kocke, 8 šestkotnih pa v istih ravninah kot stranske ploskve oktaedra.
Ameriški matematik Norman Johson (*1930) je telo imenoval omniprisekana kocka ali kantiprisekana kocka.
Kartezične koordinate
urediKartezične koordinate oglišč prisekanega kubooktaedra, ki ima dolžino roba 2 in leži v izhodišču, so vse permutacije vrednosti:
- (±1, ±(1+√2), ±(1+2√2)).
Površina in prostornina
urediPovršina P in prostornina V prisekanega oktaedra z dolžino roba a sta:
Oglišča
urediDa se poišče število oglišč, je pomembno to, da je vsako oglišče stičišče kvadrata, šestkotnika in osemkotnika.
Dualno telo
urediUniformna barvanja
urediObstaja samo ena oblika uniformnega barvanja stranskih ploskev tega poliedra. To vključuje po eno barvo za vsako stransko ploskev.
2-uniformno barvanje tudi obstaja z izmenoma obarvanimi šestkotniki.
Pravokotne projekcije
urediPrisekani kubooktaeder ima dva posebni pravokotni projekciji v Coxeterjevih ravninah A2 in B2 s projektivno simetrijo [6] in [8]. Številne simetrije se lahko konstruira iz različnih projektivnih ravnin v odvisnosti od elementov poliedrov.
| usrediščeno na | oglišče | rob 4-6 |
rob 4-8 |
rob 6-8 |
pravokotnico na stransko ploskev 4-6 |
|---|---|---|---|---|---|
| slika | |||||
| projektivna simetrija |
[2]+ | [2] | [2] | [2] | [2] |
| disdiakisni dodekaeder |
|||||
| usrediščeno na | pravokotnico na stransko ploskev – kvadrat |
pravokotnico na stransko ploskev – osemkotnik |
stransko ploskev – kvadrat |
stransko ploskev – šestkotnik |
stransko ploskev – osemkotnik |
| slika | |||||
| projektivna simetrija |
[2] | [2] | [2] | [6] | [8] |
| disdiakisni dodekaeder |
Sorodni poliedri in tlakovanja
urediVsak prisekani kubooktaeder je eden izmed članov družine uniformnih poliedrov, ki so sorodni kocki in pravilnemu oktaedru.
| {4,3} | t0,1{4,3} | t1{4,3} | t0,1{3,4} | {3,4} | t0,2{4,3} | t0,1,2{4,3} | {4,3} | h0{4,3} | h1,2{4,3} |
|---|---|---|---|---|---|---|---|---|---|
Ta polieder se lahko obravnava kot zaporedje uniformnih vzorcev, ki imajo sliko oglišč (4.6.2p) ter Coxeter-Dinkinov diagram . Za p < 6 so člani zaporedja omniprisekani poliedri (zonoedri), ki so prikazani spodaj kot sferno tlakovanje. Za p > 6 so to tlakovanja hiperbolične ravnine, ki se prične s trisedemkotnim tlakovanjem.
| simetrija | sferna | ravninska | hiperbolična | |||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] | |
| red | 12 | 24 | 48 | 120 | ∞ | |||
| omniprisekana oblika |
4.6.4 |
4.6.6 |
4.6.8 |
4.6.10 |
4.6.12 |
4.6.14 |
4.6.16 |
4.6.∞ |
| Coxeter Schläfli |
t0,1,2{2,3} |
t0,1,2{3,3} |
t0,1,2{4,3} |
t0,1,2{5,3} |
t0,1,2{6,3} |
t0,1,2{7,3} |
t0,1,2{8,3} |
t0,1,2{∞,3} |
| omniprisekani duali |
V4.6.4 |
V4.6.6 |
V4.6.8 |
V4.6.10 |
V4.6.12 |
V4.6.14 |
V4.6.16 | V4.6.∞ |
| Coxeter | ||||||||
Glej tudi
uredi- graf prisekanega kubooktaedra
- kocka
- kubooktaeder
- oktaeder
- prisekani ikozidodekaeder
- prisekani oktaeder - prisekani tetraeder
Sklici
uredi- ↑ Wenninger, Magnus (1974), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, (Model 15, p. 29)
- ↑ Cromwell, P.; Polyhedra, CUP hbk (1997), pbk. (1999). (p. 82)
- ↑ http://books.google.si/books?id=OJowej1QWpoC&lpg=PP1&pg=PA82&redir_esc=y#v=onepage&q&f=false (poglavje 3-9, s. 82)
Zunanje povezave
uredi- Weisstein, Eric Wolfgang. »Great Rhombicuboctahedron«. MathWorld.
- Trirazsežni uniformni konveksni poliedri (glej girco) (angleško)
- Uniformni poliedri (angleško)
- Virtualni poliedri v Encyclopedia of Polyhedra (angleško)
