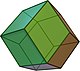
Catalanovo telo
Catalanovo telo (tudi arhimedski dual) je dualni polieder arhimedskega telesa.

Imenujejo se po belgijskem matematiku Eugènu Charlesu Catalanu (1814–1894), ki jih je prvi opisal.
Catalanova telesa so vsa konveksna. Vsa imajo prehodne stranske ploskve, niso pa ogliščnoprehodne. Vsa arhimedska telesa so ogliščnoprehodna, nimajo pa prehodnih stranskih ploskev.
V nasprotju s platonskimi telesi in arhimedskimi telesi stranske ploskve Catalanovih teles niso pravilni mnogokotniki. So pa slike oglišč Catalanovih teles pravilne in imajo stalni diedrski kot. Razen tega sta dve telesi robovnoprehodni. To sta rombski dodekaeder in rombski triakontaeder. To sta dualni telesi kvazipravilnega poliedra arhimedskih teles.
Dve od Catalanovih teles sta kiralni. To sta petkotni ikozitetraeder in petkotni heksekontaeder, ki sta dualni telesi kiralni prirezani kocki in prirezanemu dodekaedru. Vsaka od teh nastopata v dveh enanciomorfnih oblikah. Če se ne šteje enanciomorfnih oblik, je skupno 13 Catalanovih teles.
Glej tudi
urediViri
uredi- Eugène Charles Catalan Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Paris) 41, 1-71, 1865.
- Alan Holden Shapes, Space, and Symmetry. New York: Dover, 1991.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 0730208. (trinajst polpravilnih konveksnih poliedrov in njihovi duali)
Zunanje povezave
uredi- Weisstein, Eric Wolfgang. »Catalan Solid«. MathWorld.
- Catalanovo telo na Glossary for Hyperspace (angleško)
- Dualna telesa arhimedovih teles (angleško)
- Catalanova telesa (interaktivni prikaz) Arhivirano 2005-12-01 na Wayback Machine. (angleško)