Enačba
Enáčba je simbolični zapis za enakost dveh matematičnih izrazov. Izraza imenujemo leva stran in desna stran enačbe. Med njima stoji enačaj (znak =).[2][3][4]
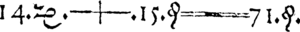
Reševanje enačbe, ki vsebuje spremenljivke, je sestavljeno iz ugotavljanja, katere vrednosti spremenljivk zadoščajo enakosti. Spremenljivke, za katere je treba enačbo rešiti, imenujemo neznanke. Rešitev enačbe je tista vrednost neznanke, za katero je vrednost leve strani enačbe enaka vrednosti desne strani enačbe.[5] Obstajata dve vrsti enačb: identične in pogojne enačbe. Če je enačba pogojna, potem velja enakost dveh izrazov za določeno vrednost spremenljivke. Če je enačba identična, je enakost veljavna za vse vrednosti, ki jih imajo spremenljivke.[6][7]
Enačba se zapiše z dvema izrazoma, povezana z znakom enakosti ("=").[8] Izrazi na obeh straneh znaka enačaja imenujejo "leva stran" in "desna stran" enačbe. Zelo pogosto velja, da je desna stran enačbe nič. To je mogoče uresničiti z odštevanjem desne strani od obeh strani.
Najpogostejša vrsta enačb je polinomska enačba (običajno imenovana tudi algebrska enačba), pri kateri sta obe strani polinoma. Strani polinomske enačbe vsebujeta enega ali več členov. Na primer enačba
ima levo stran , ki vsebuje štiri člene in desno stran , ki ga sestavlja le en člen. Imena spremenljivk kažejo, da sta x in y neznanki in da so A, B in C parametri, vendar je to običajno določeno s kontekstom (v nekaterih kontekstih je y lahko parameter; A, B in C so lahko tudi navadne spremenljivke).
Enačba je analogna tehtnici na kateri so postavljene uteži. Ko enako maso nečesa (npr. zrna) vstavimo v dve posodi, zaradi teh mas tehtnica ostane v ravnovesju, reče se da sta masi enaki. Če iz ene posode odvzamemo nekaj zrn, morate enako količino zrn odstraniti tudi iz druge posode, da ohranite tehtnico v ravnovesju. Na splošno velja, da enačba ostane v ravnovesju, če isto operacijo izvedemo na obeh straneh.
V kartezični geometriji se enačbe uporabljajo za opis geometrijskih objektov. Enačbe, ki tukaj pridejo v poštev, kot so implicitne enačbe ali parametrične enačbe, imajo neskončno veliko rešitev - namesto, da bi rešitve podali eksplicitno ali števno, kar je nemogoče, za preučevanje lastnosti objektov uporabimo enačbe. To je začetna ideja algebrske geometrije, pomembnega področja matematike.
Algebra proučuje dve glavni družini enačb: polinomske enačbe in med njimi poseben primer linearnih enačb. Kadar obstaja samo ena spremenljivka, imajo polinomske enačbe obliko P (x) = 0, kjer je P polinom, linearne enačbe pa imajo obliko ax + b = 0, kjer sta a in b parametra. Za reševanje enačb iz katere koli družine uporabimo algoritmične ali geometrijske tehnike, ki izvirajo iz linearne algebre ali matematične analize. Algebra proučuje tudi diofantinske enačbe, kjer so koeficienti in rešitve cela števila. Uporabljene tehnike so različne in izhajajo iz teorije števil. Te enačbe so na splošno težke; pogosto jih uporabljamo samo zato, da ugotovimo obstoj ali odsotnost rešitve in če ta obstaja, preštejemo število rešitev.
Diferencialne enačbe so enačbe, ki vključujejo eno ali več funkcij in njihove odvodov. Rešujejo se tako, da najdejo izraz za funkcijo, ki ne vključuje odvodov. Diferencialne enačbe se uporabljajo za modeliranje procesov, ki vključujejo hitrost spreminjanja spremenljivke. Uporabljajo se na področjih, kot so fizika, kemija, biologija in ekonomija.
Simbol " = ", ki se pojavlja v vsaki enačbi, je leta 1557 izumil Robert Recorde, ki je menil, da nič ne more biti bolj enako kot vzporedne ravni črti enake dolžine.[9]
Uvod
urediAnalogna ilustracija
urediVsaka stran enačbe ustreza eni strani tehtnice. Na vsako stran je mogoče postaviti različne količine: če so uteži na obeh straneh enake, je tehtnica v ravnovesju in po analogiji je v ravnovesju tudi enakost, ki predstavlja ravnovesje (če temu ni tako, potem pomanjkanje ravnovesja ustreza predstavljeni neenakosti z neenačbo).
Na sliki so x, y in z različne količine (v tem primeru realna števila), ki predstavljajo uteži, in vsaka od x, y in z ima drugačno maso. Seštevanje ustreza dodajanju mase, odštevanje pa odvzemanju mase od tiste, ki že obstaja. Ko velja enakost, je skupna masa na vsaki strani enaka.
Parametri in neznanke
urediEnačbe pogosto vsebujejo izraze, ki niso neznanke. Ti drugi izrazi, za katere se domneva, da so znani, se običajno imenujejo konstante, koeficienti ali parametri.
Primer enačbe, ki vključuje x in y kot neznanki, parameter R pa je
Ko parametru R izberemo vrednost 2 (R = 2), bi to enačbo lahko prepoznali v kartezičnih koordinatah kot enačbo za krog s polmerom 2 okoli izhodišča. Zato je enačba z nedoločenim R splošna enačba za krog.
Običajno so neznanke označene s črkami na koncu abecede, x, y, z, w, ...,[10] medtem ko so koeficienti (parametri) označeni s črkami iz začetka abecede, a, b, c, d ,... . Na primer, splošna kvadratna enačba se običajno zapiše ax 2 + bx + c = 0.
Postopek iskanja rešitev ali, v primeru parametrov, izražanja neznank, imenujemo reševanje enačbe. Rešitev enačbe je vsaka vrednost neznanke, za katero je vrednost leve strani enačbe enaka vrednosti desne strani enačbe.[11]
Sistem enačb je sestavljen iz dveh ali več enačb, običajno z več neznankami, za katere se išče skupne rešitve. Tako je rešitev sistema množica vrednosti za vsako neznanko, ki skupaj tvorijo rešitev vsake enačbe v sistemu. Na primer sistem
ima eno rešitev x = −1, y = 1.
Identitete
urediIdentiteta je enačba, ki velja za vse možne vrednosti spremenljivk, ki jih vsebuje; reši vsako realno število. V procesu reševanja enačbe se identiteta pogosto uporablja za poenostavitev enačbe, zaradi česar je lažje rešljiva.
V algebri je primer identitete razlika dveh kvadratov:
ki velja za vse x in y.
Trigonometrija je področje, kjer obstaja veliko identitet; te so uporabne pri manipulaciji ali reševanju trigonometričnih enačb. Dve izmed mnogih, ki vključujeta sinusno in kosinusno funkcijo, sta:
in
ki držita za vse vrednosti θ.
Na primer, da bi rešili naslednjo enačbo za vrednost θ:
kjer je θ omejena med 0 in 45 stopinj, lahko uporabimo zgornjo identiteto za produkt, da dobimo:
kar nam da naslednjo rešitev za θ:
Ker je sinusna funkcija periodična, obstaja neskončno veliko rešitev, če θ ni omejena. V tem primeru bi omejitev θ na 0 do 45 stopinj omejila rešitev le na eno število.
Lastnosti
urediDve enačbi ali dva sistema enačb sta enakovredni, če imata isto množico rešitev. Naslednje operacije pretvorijo enačbo ali sistem enačb v enakovredne - pod pogojem, da so operacije smiselne za izraze, za katere se uporabljajo:
- Seštevanje ali odštevanje iste količine na obeh straneh enačbe. To kaže, da je vsaka enačba enakovredna enačbi, v kateri je desna stran nič.
- Množenje ali deljenje obeh strani enačbe z ničelno količino.
- Uporaba identitete za preoblikovanje ene strani enačbe. Na primer: razčlenjevanje produkta ali faktoriziranje vsote.
- Za sistem: na obeh straneh enačbe prištejemo drugo stran enačbe, pomnoženo z isto količino.
Če je neka funkcija uporabljena na obeh straneh enačbe, ima nastala enačba med svojimi rešitvami rešitve prvotne enačbe, lahko pa ima tudi dodatne rešitve, imenovane lažne rešitve. Na primer enačba ima rešitev Dvig obeh strani na eksponent 2 (kar pomeni uporabo funkcije na obe strani enačbe) spremeni enačbo v , ki nima samo prejšnje rešitve, ampak uvaja tudi lažno rešitev, Poleg tega, če funkcija ni definirana pri nekaterih vrednostih (kot je 1/ x, ki ni definirana za x = 0), se lahko obstoječe rešitve pri teh vrednostih izgubijo. Zato je pri uporabi takega preoblikovanja enačbe potrebna previdnost.
Zgornje transformacije (preoblikovanja) so osnova večine elementarnih metod reševanja enačb, pa tudi nekaterih manj elementarnih, kot je Gaussova eliminacija.
Algebra
urediPolinomske enačbe
urediV splošnem je algebrska enačba oz. polinomska enačba enačba z obliko:
, ali
pri čemer sta P in Q polinoma s koeficienti v nekem polju (npr. racionalna števila, realna števila, kompleksna števila). Algebrska enačba ima lahko le eno spremenljivko. Po drugi strani pa ima lahko polinomska enačbe več spremenljivk (x, y, z, itd). Izraz polinomska enačba se običajno uporablja pogosteje kot algebrska enačba.
Na primer,
je algebrska (polinomska) enačba z eno spremenljivko koeficienti, ki so cela števila in
je polinomska enačba z več spremenljivkami z racionalnimi števili.
Nekatere (vendar ne vse) polinomske enačbe z racionalnimi koeficienti imajo rešitev, ki je algebrski izraz, s končnim številom operacij, ki vključujejo le te koeficiente (tj. lahko se jih reši algebraično). To je mogoče storiti za vse take enačbe stopnje ena, dva, tri ali štiri; za enačbe stopnje pet ali več je mogoče rešiti le nekatere, vendar kot pravi Abel -Ruffinijev izrek, ne vseh.
Sistemi linearnih enačb
urediSistem linearnih enačb (ali linearni sistem) je serija linearnih enačb, ki imajo isto množico spremenljivk. Na primer,
je sistem treh enačb s tremi spremenljivkami x, y, z. Rešitev linearnega sistema je dodelitev števil spremenljivkam na način, da so vse enačbe hkrati izpolnjene. Rešitev zgornjega sistema je
saj so pri teh vrednostih vse tri enačbe veljavne. Beseda "sistem" nakazuje, da je treba enačbe obravnavati skupaj in ne posamično.
V matematiki je teorija linearnih sistemov osnova in temeljni del linearne algebre, ki se uporablja v večini sodobne matematike. Računalniški algoritmi za iskanje rešitev so pomemben del numerične linearne algebre in imajo pomembno vlogo v fiziki, inženiringu, kemiji, računalništvu in ekonomiji. Sistem nelinearnih enačb lahko pogosto aproksimiramo z linearnim sistemom (glej linearizacijo), kar je koristna tehnika pri izdelavi matematičnega modela ali računalniške simulacije razmeroma zapletenega sistema.
Geometrija
urediAnalitična geometrija
urediV evklidski geometriji je možno povezati koordinate z vsako točko v prostoru, na primer s pomočjo ortogonalne mreže. Ta metoda omogoča, da geometrijske objekte lahko zapišemo z enačbami. Ravnino v tridimenzionalnem prostoru lahko izrazimo kot množico rešitev enačbe , kjer so in realna števila in so neznanke, ki ustrezajo koordinatam točke v sistemu v ortogonalni mreži. Vrednosti so koordinate vektorja, pravokotnega na ravnino, določenega z enačbo. Premica je izražena kot presečišče dveh ravnin, to je kot množica rešitev ene linearne enačbe z vrednostmi v ali kot množica rešitev dveh linearnih enačb z vrednostmi v
Stožčev presek je presečišče stožca z enačbo v ravnini. Z drugimi besedami, v prostoru so vsi stožci definirani kot množica rešitev enačbe ravnine in enačbe stožca. Ta formalizem omogoča določanje lege in lastnosti stožca.
Uporaba enačb omogoča reševanje geometrijskih vprašanj. Kartezični koordinatni sistem preoblikuje geometrijski problem v analitični problem, ko se liki pretvorijo v enačbe; od tod izhaja izraz analitična geometrija. Takšno stališče, ki ga je opisal Descartes, je obogatil in spremil geometrijo starogrških matematikov.
Danes je analitična geometrija za opisovanje števil še vedno uporablja enačbe, uporablja pa tudi druge tehnike, kot sta funkcijska analiza in linearna algebra.
Kartezične enačbe
urediKartezični koordinatni sistem je koordinatni sistem, ki vsako točko na ravnini enolično določi s parom numeričnih koordinat. Koordinate so razdalje od točke do dveh fiksno usmerjenih premic, ki sta označeni z enako enoto dolžine.
Po istem principu lahko določimo položaj katere koli točke v tridimenzionalnem prostoru z uporabo treh kartezičnih koordinat, ki so razdalje do treh medsebojno pravokotnih ravnin (s pravokotno projekcijo na tri medsebojno pravokotne premice).
Kartezične koordinate je v 17. stoletju izumil René Descartes (latinizirano: Cartesius), ki je revolucioniral matematiko, ko je prvič sistematično povezal evklidsko geometrijo in algebro. Z uporabo kartezičnega koordinatnega sistema lahko geometrijske oblike (na primer krivulje) opišemo z kartezičnimi enačbami: algebrske enačbe, ki vključujejo koordinate točk, ki ležijo na obliki. Na primer, krog s polmerom 2 v ravnini, s središčem na določeni točki, imenovanem izhodišče, lahko opišemo kot množico vseh točk, katerih koordinati x in y ustrezata enačbi x2 + y2 = 4.
Parametrične enačbe
urediParametrična enačba za krivuljo izraža koordinate točk krivulje kot funkcije spremenljivke, imenovane parameter.[12][13] Na primer,
sta parametrični enačbi za enotsko krožnico, kjer je t parameter.
Pojem parametrična enačba je bil posplošen na ploskve, mnogotersti in algebrske varietete višjih dimenzij, pri čemer je število parametrov enako dimenziji mnogoterosti ali varietete, število enačb pa je enako dimenziji prostora v katerem upošteva mnogoterost ali varieteta (za krivulje je dimenzija ena in uporablja se en parameter, za dimenzije ploskev je dimenzija dva in dva parametra itd.).
Reševanje enačbe
urediČe enačba vsebuje samo eno neznanko, je rešitev enačbe tista vrednost neznanke, pri kateri enačaj velja. Če enačba vsebuje n neznank, je rešitev tista n-terica vrednosti neznank, pri kateri enačaj velja. Enačba ima lahko tudi več rešitev (več vrednosti neznanke oziroma več n-teric, pri katerih enačaj velja).
Zgled: enačba x2 = 5x − 6 ima dve rešitvi: x1 = 2, x2 = 3.
Če je enakost veljavna pri poljubnih vrednostih neznank, taki enačbi rečemo identična enačba (krajše identiteta).
Zgled identične enačbe: (x + 1)2 = x2 + 2x + 1. Rešitev te enačbe je poljubno število x.
Enačba, ki nima rešitve, se imenuje nerešljiva enačba. Zgled: x + 1 = x + 2.
Enačbi, ki imata enaki množici rešitev, sta med seboj enakovredni ali ekvivalentni. Zgled enakovrednih enačb: 3x = 6 in x + 1 = 3.
Reševanje enačbe pomeni iskanje rešitev enačbe. Reševanje poteka običajno tako, da enačbo preoblikujemo v drugo obliko, ki pa je prvotni enakovredna. Pri tem lahko uporabimo naslednje postopke:
- preoblikujemo samo levo ali pa samo desno stran po pravilih za preoblikovanje izrazov (odpravljanje oklepajev, ureditev členov ipd)
- na levi in desni strani lahko prištejemo isto število
- na levi in desni strani lahko odštejemo isto število
- levo in desno stran lahko pomnožimo z istim številom, ki pa ne sme biti enako 0
- levo in desno stran lahko delimo z istim številom, ki pa ne sme biti enako 0
- na levi in desni strani lahko izvedemo isto matematično funkcijo, ki pa mora biti bijektivna (npr.: kubiranje)
Če levo in desno stran pomnožimo ali delimo z matematičnim izrazom, ki bi lahko bil enak 0 (za določeno vrednost spremenljivke), dobljena enačba ni nujno enakovredna prvotni. Če na levi in desni strani izvedemo funkcijo, ki ni bijektivna (npr.: kvadriranje), dobljena enačba ni nujno enakovredna prvotni. Takim postopkom se pri reševanju enačb poskušamo izogniti.
Vrste enačb
urediEnačbe je mogoče razvrstiti glede na vrste operacij in količine. Najbolj znane vrste enačb so:
- Algebrska enačba ali polinomska enačba je enačba, pri kateri sta obe strani polinoma (glej tudi sistem polinomskih enačb). Te so nadalje razvrščene po stopnjah:
- linearna enačba za prvo stopnjo
- kvadratna enačba za drugo stopnjo
- kubična enačba za tretjo stopnjo
- kvartična enačba za četrto stopnjo
- kvintična enačba za peto stopnjo
- sekstična enačba za stopnjo šest
- septična enčba za stopnjo sedem
- oktična enačba za osmo stopnjo
- Diofantinska enačba je enačba, pri kateri morajo biti neznanke cela števila
- Transcendentalna enačba je enačba, ki vključuje transcendentalno funkcijo svojih neznank
- Parametrična enačba je enačba, v kateri so rešitve spremenljivk izražene kot funkcije nekaterih drugih spremenljivk, imenovanih parametri, ki se pojavljajo v enačbah
- Funkcijska enačba je enačba, v kateri so neznanke funkcije in ne preproste količine
- Enačbe, ki vključujejo odvode, integrale in končne razlike:
- Diferencialna enačba je funkcijska enačba, ki vključuje odvode neznanih funkcij, kjer so funkcija in njeni odvodi ovrednoteni na isti točki, kot je npr. . Diferencialne enačbe so razdeljene na navadne diferencialne enačbe za funkcije ene spremenljivke in parcialne diferencialne enačbe za funkcije z več spremenljivkami
- Integralska enačba je funkcijska enačba, ki vključuje primitivne funkcije neznanih funkcij.
- Integralno-diferencialna enačba je funkcijska enačba, ki vključuje tako odvode kot tudi primitivne funkcije neznanih funkcij.
- Funkcijska diferencialna enačba zakasnitvene diferencialne enačbe je enačba funkcije, ki vključuje odvode neznanih funkcij, ovrednotene na več točkah, kot je npr.
- Diferenčna enačba je enačba, kjer je neznanka funkcija f, ki se pojavi v enačbi preko f (x), f (x −1), ..., f (x - k), za neko celo število k, imenovano vrstni red enačbe. Če je x omejeno na celo število, je diferenčna enačba enaka rekurzivni zvezi
Najbolj znana enačba na svetu je verjetno Einsteinova .
Posebna vrsta enačbe je matematična formula ali obrazec: to je enačba, ki podaja navodilo za izračunavanje neke količine s pomočjo ustreznih podatkov, npr.: formula za površino krogle s polmerom r je: .
Glej tudi
urediOpombe
uredi- ↑ Lahko se zapiše tudi kot P – Q = 0.
Sklici
uredi- ↑ Recorde, Robert, The Whetstone of Witte … (London, England: Jhon Kyngstone, 1557), the third page of the chapter "The rule of equation, commonly called Algebers Rule."
- ↑ »Compendium of Mathematical Symbols«. Math Vault (v ameriški angleščini). 1. marec 2020. Pridobljeno 1. septembra 2020.
- ↑ »Equation - Math Open Reference«. www.mathopenref.com. Pridobljeno 1. septembra 2020.
- ↑ »Equations and Formulas«. www.mathsisfun.com. Pridobljeno 1. septembra 2020.
- ↑ »Rešitev enačbe«. eucbeniki.sio.si. Arhivirano iz prvotnega spletišča dne 10. septembra 2021. Pridobljeno 10. septembra 2021.
- ↑ Lachaud, Gilles. »Équation, mathématique«. Encyclopædia Universalis (v francoščini).
- ↑ "A statement of equality between two expressions. Equations are of two types, identities and conditional equations (or usually simply "equations")". « Equation », in Mathematics Dictionary, Glenn James (mathematician) et Robert C. James (éd.), Van Nostrand, 1968, 3 ed. 1st ed. 1948, str. 131.
- ↑ »Equation - Math Open Reference«. www.mathopenref.com. Pridobljeno 1. septembra 2020.
- ↑ Recorde, Robert, The Whetstone of Witte … (London, England: Jhon Kyngstone, 1557), the third page of the chapter "The rule of equation, commonly called Algebers Rule."
- ↑ »Compendium of Mathematical Symbols«. Math Vault (v ameriški angleščini). 1. marec 2020. Pridobljeno 1. septembra 2020.
- ↑ »Reševanje enačb«. eucbeniki.sio.si. Arhivirano iz prvotnega spletišča dne 11. septembra 2021. Pridobljeno 11. septembra 2021.
- ↑ Thomas, George B., and Finney, Ross L., Calculus and Analytic Geometry, Addison Wesley Publishing Co., fifth edition, 1979, p. 91.
- ↑ Weisstein, Eric W. "Parametric Equations." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ParametricEquations.html
Zunanje povezave
uredi- Winplot: General Purpose plotter that can draw and animate 2D and 3D mathematical equations.
- Equation plotter: A web page for producing and downloading pdf or postscript plots of the solution sets to equations and inequations in two variables (x and y).


