Mala in velika polos
V geometriji je velika os elipse njen največji premer: daljica, ki poteka skozi središče in obe gorišči s koncema na najširšima deloma roba.
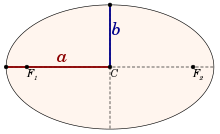
Velika polos je ena polovica večje osi, in torej teče od središča, skozi gorišče in do roba. Mala polos elipse ali hiperbola je daljica, ki je pravokotna na veliko polos in ima en konec na središču stožnice. Za posebni primer, krog, sta obe polosi enako dolgi, to je polmer kroga.
Dolžina velike polosi a elipse je povezana z dolžino male polosi b, ekscentičnostjo e in pol-latus rectum , kot sledi:
Velika polos hiperbole je, odvisno od dogovora, plus ali minus ene polovice razdalje med obema vejama. Torej je to razdalja od središča do enega od temen hiperbole.
Parabola se lahko izrazi kot limito sekvence elips, kjer je eno gorišče stalno, drugo pa se lahko odmika v eno smer, a ohrani stalen. Torej a in b silita k neskončnosti, a hitreje kot b.
Velika in mala os sta osi simetrije krivulje: v elipse je mala os krajša; v hiperboli je takšna, ki krivulje ne seka.
Elipsa
urediEnačba za elipso je:
Kjer je (h,k) središče elipse v kartezičnih koordinatah, v katerih je določena točka podana z (x,y).
Velika polos je srednja vrednost maksimalne in minimalne razdalje in elipse od gorišča — torej razdalji od gorišča do končnih točk na nasprotnih smereh.[navedi vir] V astronomiji se te ekstremne točke imenujejo apside.[1]
Mala polos elipse je geometrična sredina teh razdalj:
Ekscentričnost elipse je definirana z
- so .
Sedaj oblikujmo enačbo v polarnih koordinatah z enim goriščem na izhodišču ter drugim na smeri ,
Srednja vrednost od in za in je
V elipsi je velika polos geometrična sredina razdalje od središča do kateregakoli izmed gorišč in razdalje od središča do ene izmed direktriks.
Mala polos elipse teče od središča elipse (točka na sredini črte med goriščema) do roba elipse. Mala polos je polovica male osi. Mala os je najdaljša daljica, ki je pravokotna na veliko polos, ki povezuje nasprotna pola elipse.
Mala polos b je z veliko polosjo a, ekscentričnostjo e in pol-latus rectum povezana tako:
Parabola se lahko izrazi kot limito serije elips, kjer je eno gorišče stalno, drugo pa se lahko odmika v eno smer, a ohrani stalen. Torej a in b silita k neskončnosti, a hitreje kot b.
Dolžina male polosi se lahko odkrije tudi z uporabo formule,[2]
kjer je f razdalja med goriščema, p in q pa sta razdalji od vsakega gorišča do katerekoli točke v elipsi.
Hiperbola
urediVelika polos hiperbole je, odvisno od dogovora, plus ali minus ena polovica razdalje med obema temenoma; če je to a v smeri x, potem je enačba:
Mala in velika polos sta skozi ekscentričnost povezani, kot sledi:
V hiperboli je lahko b tudi večji od a. [1]
Astronomija
urediOrbitalna perioda
urediV astrodinamiki je orbitalna perioda T malega telesa, ki kroži okoli središčnega telesa v krožni ali eliptični orbiti enaka:[1]
kjer:
- a je dolžina velike polosi orbite
- je standardni gravitacijski parameter središčnega telesa
Velja omeniti, da je za vse elipse z enako veliko polosjo orbitalna perioda enaka, ne glede na njihovo ekscentričnost.
Specifična vrtilna količina h malega telesa, ki kroži okoli središčnega telesa v krožni ali eliptični orbiti je:[1]
kjer:
- a in sta definirana zgoraj
- e je ekscentričnost orbite
V astronomiji je velika polos eden izmed najpomembnejših orbitalnih elementov tirnice, skupaj z orbitalno periodo. Za telesa v Osončju je velika polos povezana s periodo po Keplerjevem tretjem zakonu (originalno empirično izpeljanem),[1]
kjer je T perioda in a je velika polos. Izkaže se, da je izrek le poenostavitev splošnega problema dveh teles, kot je to določil Newton:[1]
kjer je G gravitacijska konstanta, M je masa središčnega telesa in m je masa krožečega telesa. Po navadi je masa središčnega telesa tolikokrat večja od manjšega, da m zanemarimo. Če uporabimo ta sklep in običajne astronomske enote, odkrijemo zakon, ki ga je prej že empirično odkril Kepler.
Pot krožečega telesa okoli baricentra in njegova pot, relativna na primarno gorišče, sta elipsi.[1] Velika polos se v astronomiji pogosto definira kot razdalja med obema telesoma, saj je navadno razmerje mas primarnega proti sekundarnemu telesu zelo veliko ( ); iz tega sledi, da se orbitalni parametri pogosto podajajo v heliocentričnih koordinatah. Razlika med primocentričnimi in "absolutnimi" orbitami se lahko najbolje ilustrira s sistemom Zemlja-Luna. Masno razmerje je v tem primeru 81,30059. Karakteristična razdalja Zemlja-Luna, velika polos geocentrične lunarne orbite, je 384.400 km. (Ob podatku ekscentričnosti lunine orbite e = 0,0549 dobimo za malo polos dolžino 383.800 km. Torej je Lunina orbita skoraj krožna.) Baricentrična lunarna orbita pa ima za razliko od prve, veliko polos enako 379.730 km zaradi obratne orbite Zemlje se odšteje razlika 4.670 km. Lunina povprečna baricentrična orbitalna hitrost je 1,010 km/s, medtem ko je Zemljina enaka 0,012 km/s. Seštevek obeh hitrosti nam poda povprečno lunino orbitalno hitrost 1,022 km/s; enaka vrednost se lahko dobi tudi z upoštevanjem le geocentrične vrednosti velike polosi.
Povprečna razdalja
urediPogosto se reče, da velika polos ni "povprečna" razdalja med primarnim goriščem elipse in krožečim telesom. To pa ni popolnoma pravilno, saj je to odvisno od tega, kaj mislimo, da je povprečno.
- povprečje nad ekscentrično anomalijo seveda sledi v veliko polos.
- povprečje nad pravo anomalijo (pravi orbitalni kot, merjen od gorišča) vodi v malo polos .
- povprečje nad srednjo anomalijo (delež orbitalne periode, ki je minila od pericentra, izražena kot kot), končno, poda časovno-povprečni
Časovno-povprečna vrednost recipročne vrednosti polmera je .
Energija; izračun velike polosi iz položajnih vektorjev
urediV astrodinamiki se lahko velika polos a izračuna iz orbitalnih položajnih vektorjev:
za eliptično orbito ali, odvisno od dogovora, je
in
(specifična orbitalna energija)
in
(standardni gravitacijski parameter), kjer:
- v je orbitalna hitrost iz hitrostnega vektorja krožečega telesa,
- r je kartezični položajni vektor krožečega telesa v koordinatah opazovalnega sistema glede na katere elemente v orbiti mora izračunati (tj. geocentrični ekvatorialni za orbito okoli Zemlje, ali heliocentrične ekliptične za orbito okoli Sonca),
- G je gravitacijska konstanta,
- M je masa gravitacijskega telesa in
- je specifična energija krožečega telesa.
Omenimo še, da za dano vrednost mase, sta specifična energija in velika polos vedno enaki, ne glede na ekscentričnost ali na razmerje mas. Obratno, za podano skupno maso in veliko polos, je skupna specifična orbitalna energija vedno enaka. Ta izjava bo vedno držala, ne glede na katerekoli pogoje.
Velike in male polosi planetov
uredi| Ime | Eksentričnost | Velika polos a (AU)| | Mala polos b (AU) | razlika (%) | Perihelij (AU) | Afelij (AU) | razlika (%) |
|---|---|---|---|---|---|---|---|
| Merkur | 0,206 | 0,38700 | 0,37870 | 2,2 | 0,307 | 0,467 | 52 |
| Venera | 0,007 | 0,72300 | 0,72298 | 0,002 | 0,718 | 0,728 | 1,4 |
| Zemlja | 0,017 | 1,00000 | 0,99986 | 0,014 | 0,983 | 1,017 | 3,5 |
| Mars | 0,093 | 1,52400 | 1,51740 | 0,44 | 1,382 | 1,666 | 21 |
| Jupiter | 0,049 | 5,20440 | 5,19820 | 0,12 | 4,950 | 5,459 | 10 |
| Saturn | 0,057 | 9,58260 | 9,56730 | 0,16 | 9,041 | 10,124 | 12 |
| Uran | 0,046 | 19,21840 | 19,19770 | 0,11 | 18,330 | 20,110 | 9,7 |
| Neptun | 0,010 | 30,11000 | 30,10870 | 0,004 | 29,820 | 30,400 | 1,9 |
Glej tudi
urediViri
uredi- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 Lissauer, Jack J.; de Pater, Imke (2019). Fundamental Planetary Sciences : physics, chemistry, and habitability. New York, NY, USA: Cambridge University Press. str. 24–31. ISBN 9781108411981.
- ↑ http://www.mathopenref.com/ellipseaxes.html,"Major[mrtva povezava] / Minor axis of an ellipse",Math Open Reference, 12 May 2013
- ↑ »The Geometry of Orbits: Ellipses, Parabolas, and Hyperbolas«. www.bogan.ca.
Zunanje povezave
uredi- Velika in mala polos elipse Z interaktivno animacijo

