Polarni koordinatni sistem
Polárni koordinátni sistém je ravninski koordinatni sistem, ki se ga uporablja v matematiki, fiziki, astronomiji in nekatrih drugih vedah. Uporabljamo ga kot alternativo kartezičnemu koordinatnemu sistemu. Polarni koordiantni sistem je tudi osnova za dva koordinatna sistema v prostoru: cilindrični in sferni koordinatni sistem.

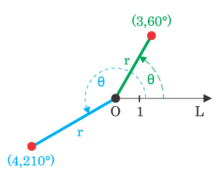

Točko v polarnem koordinatnem sistemu podamo z dvema številoma, ki ju imenujemo polarni koordinati:
- prva koordinata točke je radij (točke oddaljenost od izhodišča) - po navadi ga označimo s črko r, včasih pa tudi z ρ. Radij je praviloma večji od 0, le v izhodišču je r = 0.
- druga koordinata točke je polarni kot - označimo ga s črko φ ali θ. To je kot, ki ga določa točka glede na desni del vodoravne osi. Polarni kot je pozitiven, če ga merimo v matematično pozitivni smeri (v obratni smeri urinih kazalcev), in negativen, če ga merimo v matematično negativni smeri (v smeri urinih kazalcev). Polarni kot se po navadi podaja na intervalu [0°,360°] ali pa na intervalu (-180°,180°]. Pogosto se ga podaja tudi v radianih.
Pretvorba koordinat
urediČe poznamo polarni koordinati točke, lahko izračunamo njeni kartezični koordinati x in y z zvezama:
Če poznamo kartezični koordinati, pa lahko dobimo polarni koordinati s pomočjo enačb:
Iz spodnje enačbe dobimo polarni kot φ s pomočjo funkcije arkus tangens - pri tem moramo paziti na pravilno izbiro vrednosti kota (po potrebi moramo prišteti +180°). Večina sodobnih kalkulatorjev ima že vgrajeno pretvorbo koordinat, ki avtomatično izračuna pravilni kot: tipka R→P pomeni pretvorbo iz pravokotnih v polarne koordinate (angleško Rectangular → Polar), tipka P→R pa obratno.
Polarne koordinate vektorjev
urediTudi ravninske vektorje lahko podajamo s polarnimi koordinatami. Pri tem r pomeni dolžino vektorja, φ pa njegovo smer (smerni kot).
Vektor, ki ima dolžino r in smerni kot φ, lahko zapišemo s kartezičnimi koordinatami kot:
Polarne koordinate kompleksnih števil
urediKompleksno število z = x + iy geometrijsko predstavimo s točko v ravnini. Če to točko opišemo s polarnima koordiantama, lahko rečemo, da smo kompleksnemu številu priredili polarni koordinati. Polarna koordinata r pri tem pomeni absolutno vrednost kompleksnega števila z. Polarno koordinato φ pri kompleksnih številih imenujemo tudi argument števila z in ga praviloma podajamo v radianih.
Kompleksno število, ki ima absolutno vrednost r in argument (polarni kot) φ, je torej enako:
Če upoštevamo Eulerjevo enačbo lahko to pišemo tudi kot:
Polarne koordinate so povezane z množenjem in deljenjem kompleksnih števil:
- Pri množenju dveh kompleksnih števil se obe absolutni vrednosti zmnožita, polarna kota pa se seštejeta.
- Pri deljenju dveh kompleksnih števil se obe absolutni vrednosti delita, polarna kota pa se odštejeta.