Oktaedrska simetrija

točkovne grupe v treh razsežnostih
poliedrska grupa, [n,3], (*n32)
involucijska simetrija C_s, [1], (*)	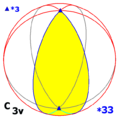ciklična simetrija C_nv, [n], (*nn)	diedrska simetrija D_nh, [n,2], (*n22)
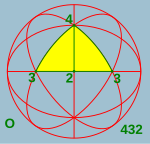
tetraedrska simetrija T_d, [3,3], (*332)	oktaedrska simetrija O_h, [4,3], (*432)	ikozaedrska simetrija I_h, [5,3], (*532)

Oktaedrska simetrija je simetrija pravilnega oktaedra. To je simetrija, ki ohranja orientacijo. Ima red simetrije enak 48, kar vključuje tudi preslikave, ki vključujejo zrcaljenje in vrtenje. Kocka ima enako skupino simetrij, ker je dualno telo oktaedra.

Kocka je najbolj znana oblika z oktaedrsko simetrijo.

Podrobnosti

Kiralna in polna (akiralna) oktaederska simetrija so točkovne grupne simetrije ali simetrije na sferi z največjo simetrijskimi grupami, ki so primerljive s translacijsko simetrijo. So med kristalne točkovne grupe kubičnega kristalnega sistema.

Kiralna oktaederska simetrija

O, 432 ali [4,3]⁺ reda 24 so kiralni oktaedersko simetrijo ali vrtilno oktaedersko simetrijo. Ta grupa je podobna kiralni tetraedrski simetriji T, toda C₂ postanejo osi C₄ ter šest dodatnih osi C₂ s srednjimi točkami robov kocke. T_d im O sta izomorfni kot abstraktni grupi, obe odgovarjata S₄, ki je simetrijska grupa za štiri objekte. T_d je unija T in množice, ki jo dobimo tako, da kombiniramo vsak element O \ T z inverzijo. O je vrtilna grupa kocke in pravilnega oktaedra.

Podgrupe kiralne oktaederske simetrije

Schönfliesova notacija	Coxeterjeva notacija	notacija orbifold	Hermann Mauguinova notacija	Order	indeks
O	[4,3]⁺	432	432	24	1
T	[3,3]⁺	332	23	12	2
D₄	[4,2]⁺	422	422	8	3
D₃	[3,2]⁺	322	322	6	4
D₂	[2,2]⁺	222	222	4	6
C₄	[4]⁺	44	4	4	6
C₃	[3]⁺	33	3	3	8
C₂	[2]⁺	22	2	2	12
S₁	[ ]⁺	11	1	1	24

Konjugirani razredi

inverzija
6 x zrcaljenje z vrtenjem za 90º
8 x zrcaljenje z vrtenjem za 60º
3 x zrcaljenje v ravnini pravokotni z 4-kratno osjo
6 x zrcaljenje v ravnini pravokotni z 2-kratno osjo

Akiralna oktaederska simetrija

O_h, *432, [4,3]⁺ ali m3m reda 48 ima akiralno oktaedersko simetrijo ali polno oktaedersko simetrijo. Ta grupa ima enake vrtilne osi kot so O, ampak in s tem imajo izčrpne zrcalne ravnine T_h in T_h. Ta grupa je izomorfna z S₄.C₄ in je tako polna simetrijska grupa kocke in oktaedra. Je hiperoktaederska grupa za n=3.

Telo kocka-oktaeder.	Vsaka stranska ploskev tega disdiakisnega dodekaedra je osnovna domena	Oktaedrska grupa O_h z osnovno domeno

Z 4-kratnimi osmi kot koordinatnimi osmi je osnovna domena O_h dana z 0 ≤ x ≤ y ≤ z. Za objekte s to simetrijo je značilen del objekta v osnovni domeni, kot je na primer kocka je dana z z = 1 in za oktaeder z x + y +z =1.

Podgrupe polne oktaederske simetrije

Schönfliesova notacija	Coxeterjeva notacija	notacija orbifold	Hermann Mauguinova notacija	red	indeks
O_h	[4,3]	*432	m3m	48	1
O	[4,3]⁺	432	432	24	2
T_d	[3,3]	*332	43m	24	2
T_h	[4,3⁺]	3*2	m3	24	2
D_4h	[4,2]	*422	4/mmm	16	3
T	[3,3]⁺	332	23	12	4
D_3d	[2⁺,6]	2*3	3m	12	4
D_2d	[2⁺,4]	2*2	42m	8	6
D₄	[4,2]⁺	422	422	8	6
C_4h	[4⁺,2]	4*	4/m	8	6
C_4v	[4]	*44	4mm	8	6
D_2h	[2,2]	*222	mmm	8	6
D₃	[3,2]⁺	322	32	6	8
C_3v	[3]	*33	3m	6	8
S₆	[2⁺,6⁺]	3×	3	6	8
D₂	[2,2]⁺	222	222	4	12
C_2h	[2,2⁺]	2*	2/m	4	12
C_2v	[2]	*22	mm2	4	12
C₄	[4]⁺	44	4	4	12
S₄	[2⁺,4⁺]	2×	8	4	12
C₃	[3]⁺	33	3	3	16
C₂	[2]⁺	22	2	2	24
S₂	[2⁺,2⁺]	×	1	2	24
C_s	[ ]	*	2 or m	2	24
C₁	[ ]⁺	11	1	1	48

Konjugirani razredi

identiteta
6 x vrtenje za 90º
8 x vrtenje za 120º
3 x vrtenje za 180º okoli 4-kratne osi
3 x vrtenje za 180º okoli 2-kratne osi

Oktaederska simetrija Bolzove ploskve

V teoriji Riemannove ploskve se včasih [[Bolzova ploskev imenuje Bolzova krivulja. Dobimo jo kot košato dvojno pokrivalo Riemannove sfere z delitvijo na množico oglišč pravilnega včrtanega oktaedra. Njegove grupe avtomorfizma hipereliptično vključevanje, ki razpade v dva dela , ki se prekrivata. Kvocient z redom podgrupe 2, ki je generirana s hipereliptičnim vključevanjem nam da natančno grupo simetrij oktaedra. Med mnogimi pomembnimi lastnostmi Bolzovih ploskev je lastnost, ki nam da največjo sistolo med vsemi hiperboličnimi ploskvami, z rodom 2.

Telesa z oktaedersko kiralno simetrijo

Skupina	Ime	Slika	Stranske ploskve	Robovi	Oglišča
arhimedsko telo	prirezana kocka		38	60	24
Catalanovo telo	petstrani ikozitetraeder		24	60	38

Telesa s polno oktaedersko simetrijo

Skupina teles	Ime	Stranske ploskve	Robovi	Oglišča
platonsko telo	kocka	6	12	8
platonsko telo	oktaeder	8	12	6
arhimedsko telo	kubooktaeder	14	24	12
	prisekana kocka	14	36	24
	prisekan oktaeder	14	36	24
	rombikubooktaeder	26	48	24
	prisekani kubooktaeder	26	72	48
Catalanovo telo	rombski dodekaeder	14	24	12
	triakisni oktaeder	24	36	14
	tetrakisni heksaeder	24	36	14
	deltoidni ikozitetraeder	24	48	26
	disdiakisni dodekaeder	48	72	26
pravilni sestav poliedrov	stela oktangula	8	12	8
pravilni sestav poliedrov	kocka in oktaeder	14	24	14

Glej tudi

Zunanje povezave

Oktaederska grupa (O) (slovensko)
Oktaederska grupa na MathWorld (angleško)
Oktaederska simetrija^{[mrtva povezava]} (angleško)