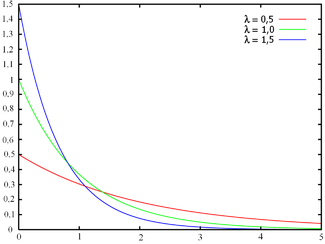
Eksponentna porazdelitev je družina zveznih verjetnostnih porazdelitev . Opisuje časovne intervale med posameznimi dogodki v Poissonovi porazdelitvi . To so procesi, ki se enakomerno pojavljajo nepretrgoma in neodvisno.
Eksponentna porazdelitev
Funkcija gostote verjetnosti za eksponentno porazdelitev.
Zbirna funkcija verjetnosti za eksponentno porazdelitev.
oznaka
E
x
p
(
λ
)
{\displaystyle Exp(\lambda )\!}
parametri
λ
>
0
{\displaystyle \lambda >0\,}
parameter stopnje realno število )
interval
[
0
,
∞
)
{\displaystyle [0,\infty )\!}
funkcija gostote verjetnosti
λ
e
−
λ
x
{\displaystyle \lambda e^{-\lambda x}\!}
zbirna funkcija verjetnosti
1
−
e
−
λ
x
{\displaystyle 1-e^{-\lambda x}\!}
pričakovana vrednost
1
λ
{\displaystyle {\frac {1}{\lambda }}\,}
mediana
ln
(
2
)
λ
{\displaystyle {\frac {\ln(2)}{\lambda }}\,}
modus
0
{\displaystyle 0\,}
varianca
1
λ
2
{\displaystyle {\frac {1}{\lambda ^{2}}}\,}
simetrija
2
{\displaystyle 2\,}
sploščenost
6
{\displaystyle 6\,}
entropija
1
−
ln
(
λ
)
{\displaystyle 1-\ln(\lambda )\,}
funkcija generiranja momentov
(
1
−
t
λ
)
−
1
{\displaystyle \left(1-{\frac {t}{\lambda }}\right)^{-1}\,}
karakteristična funkcija
(
1
−
i
t
λ
)
−
1
{\displaystyle \left(1-{\frac {it}{\lambda }}\right)^{-1}\,}
Funkcija gostote verjetnosti
uredi
Funkcija gostote verjetnosti za eksponentno porazdelitev je
f
(
x
;
λ
)
=
{
λ
e
−
λ
x
,
x
≥
0
,
0
,
x
<
0.
{\displaystyle f(x;\lambda )=\left\{{\begin{matrix}\lambda e^{-\lambda x},&\;x\geq 0,\\0,&\;x<0.\end{matrix}}\right.}
kjer je
λ
>
0
{\displaystyle \lambda >0\!}
parameter stopnje (obratna vrednost parametra merila). Zbirna funkcija verjetnosti
uredi
Zbirna funkcija verjetnosti je enaka
F
(
x
;
λ
)
=
{
1
−
e
−
λ
x
,
x
≥
0
,
0
,
x
<
0.
{\displaystyle F(x;\lambda )=\left\{{\begin{matrix}1-e^{-\lambda x},&\;x\geq 0,\\0,&\;x<0.\end{matrix}}\right.}
uredi
Pričakovana vrednost je enaka
1
λ
{\displaystyle {\frac {1}{\lambda }}\,}
Varianca je enaka
1
λ
2
{\displaystyle {\frac {1}{\lambda ^{2}}}\,}
Funkcija generiranja momentov
uredi
uredi
Povezave z drugimi porazdelitvami
uredi
Minimum neodvisnih slučajnih spremenljivk , ki so porazdeljene eksponentno, je tudi eksponentno porazdeljena slučajna spremenljivka. Naj bodo
X
1
,
…
,
X
n
{\displaystyle X_{1},\ldots ,X_{n}\!}
X
i
∼
E
x
p
(
λ
i
)
{\displaystyle X_{i}\sim \mathrm {Exp} (\lambda _{i})\!}
Y
=
min
i
=
1
,
…
,
n
(
X
i
)
{\displaystyle Y=\min \limits _{i=1,\ldots ,n}(X_{i})\!}
Y
∼
E
x
p
(
∑
i
=
1
n
λ
i
)
{\displaystyle Y\sim \mathrm {Exp} \left(\sum \limits _{i=1}^{n}\lambda _{i}\right)}
Eksponentna porazdelitev je posebni primer porazdelitve gama
E
x
p
(
λ
)
≡
Γ
(
1
,
1
/
λ
)
{\displaystyle \mathrm {Exp} (\lambda )\equiv \Gamma (1,1/\lambda )\!}
Vsota neodvisnih eksponentnih porazdelitev ima gama porazdelitev. Naj bodo
X
1
,
…
,
X
n
{\displaystyle X_{1},\ldots ,X_{n}\!}
X
i
∼
E
x
p
(
λ
i
)
{\displaystyle X_{i}\sim \mathrm {Exp} (\lambda _{i})\!}
Y
=
∑
i
=
1
n
X
i
∼
Γ
(
n
,
λ
)
{\displaystyle Y=\sum \limits _{i=1}^{n}X_{i}\sim \Gamma (n,\lambda )\!}
Eksponentna porazdelitev s parametrom
λ
=
1
/
2
{\displaystyle \lambda =1/2\!}
porazdelitve hi-kvadrat
E
x
p
(
1
/
2
)
≡
χ
2
(
2
)
{\displaystyle \mathrm {Exp} (1/2)\equiv \chi ^{2}(2)\!}
Za slučajno spremenljivko
Y
{\displaystyle Y\!}
Weibullovo porazdelitev , lahko zapišemo
Y
∼
Weibull
(
γ
,
λ
)
{\displaystyle Y\sim \operatorname {Weibull} (\gamma ,\lambda )}
Y
=
X
1
/
γ
{\displaystyle Y=X^{1/\gamma }\,}
X
{\displaystyle X\!}
X
∼
Exp
(
λ
−
γ
)
{\displaystyle X\sim \operatorname {Exp} (\lambda ^{-\gamma })}
Slučajna spremenljivka
Y
{\displaystyle Y\!}
Rayleighovo porazdelitev , kar lahko zapišemo kot
Y
∼
Rayleigh
(
σ
)
{\displaystyle Y\sim \operatorname {Rayleigh} (\sigma )}
Y
=
2
X
σ
2
λ
{\displaystyle Y={\sqrt {2X\sigma ^{2}\lambda }}}
X
{\displaystyle X\!}
X
∼
Exp
(
λ
)
{\displaystyle X\sim \operatorname {Exp} (\lambda )}
Če ima slučajna spremenljivka
Y
{\displaystyle Y\!}
Gumbelovo porazdelitev , kar lahko zapišemo kot
Y
∼
Gumbel
(
μ
,
β
)
{\displaystyle Y\sim \operatorname {Gumbel} (\mu ,\beta )}
Y
=
μ
−
β
log
(
X
/
λ
)
{\displaystyle Y=\mu -\beta \log(X/\lambda )\,}
X
{\displaystyle X\!}
X
∼
Exp
(
λ
)
{\displaystyle X\sim \operatorname {Exp} (\lambda )}
Slučajna spremenljivka
Y
{\displaystyle Y\!}
Laplaceovo porazdelitev , kar lahko zapišemo kot
Y
∼
Laplace
{\displaystyle Y\sim \operatorname {Laplace} }
X
1
{\displaystyle X_{1}\,}
X
2
{\displaystyle X_{2}\,}
Y
=
X
1
−
X
2
{\displaystyle Y=X_{1}-X_{2}\,}