Obseg (teorija grafov)

Za druge pomene glej obseg (razločitev).

Obseg v teoriji grafov pomeni dva pojma. Notranji obseg (angleško girth) grafa je dolžina njegovega najkrajšega cikla. Če graf ne vsebuje ciklov (je aciklični graf), je njegov notranji obseg po definiciji enak neskončnosti. Notranji obseg 4-cikla (kvadrata) je 4. Notranji obseg mreže je tudi enak 4, trikotniške mreže pa enak 3. Graf z notranjih obsegom večjim od 3 nima trikotnikov. Zunanji obseg (angleško circumference) grafa je dolžina njegovega najdaljšega cikla. Obsega predstavljata invarianti grafa.

• 
  Notranji obseg Fruchtovega grafa je 3
• 
  Notranji obseg vsakega polnega grafa $K_{n}$ pri $n\geq 3$ je 3. Na sliki polni graf $K_{12}$
• 
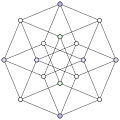
  Notranji obseg hiperkockinega grafa je 4
• 
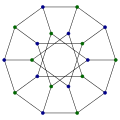
  Notranji obseg Higman-Simsovega grafa je 4
• 
  Notranji obseg Desarguesovega grafa je 6
• 
  Notranji obseg Biggs-Smithovega grafa je 9
• 
  Notranji obseg Ljubljanskega grafa je 10

Kletke

Kubični graf (vse njegove točke imajo stopnjo 3) z notranjim obsegom $g$, ki je majhen kolikor je mogoče, je znan kot $g$-kletka (ali kot (3,g)-kletka). Petersenov graf je edina 5-kletka (je najmanjši kubični graf z notranjim obsegom 5), Heawoodov graf je edina 6-kletka, McGeejev graf je edina 7-kletka, Tuttejeva osmera kletka pa je edina 8-kletka. Za dani notranji obseg lahko obstaja več kletk. Obstajajo na primer tri neizomorfne 10-kletke, vsaka s 70-timi točkami: Balabanova 10-kletka, Harriesov graf in Harries-Wongov graf.

• 
  Notranji obseg Petersenovega grafa je 5
• 
  Notranji obseg Heawoodovega grafa je 6
• 
  Notranji obseg McGeejevega grafa je 7
• 
  Notranji obseg Tuttejeve osmere kletke je 8

Notranji obseg in barvanje grafa

Za poljubni pozitivni celi števili g in χ obstaja graf z notranjim obsegom vsaj g in kromatičnim številom vsaj χ. Grötzschev graf na primer nima trikotnikov, njegovo kromatično število je enako 4. S ponavljanjem konstrukcije Mycielskega lahko iz Grötzschevega grafa dobimo grafe brez trikotnikov s poljubno velikim kromatičnim številom. Paul Erdős je prvi dokazal splošni rezultat s pomočjo verjetnostne metode. Pokazal je, da naključni graf na n točkah, ki je nastal z neodvisno izbiro vsake povezave z verjetnostjo n^{(1 − g)/g}, ima, če verjetnost teži k 1, ko gre n k neskončnosti, največ n/2 ciklov dolžine g ali manj, vendar nima neodvisne množice velikosti n/2k. Če odstranimo eno točko iz vsakega kratkega cikla, zato dobimo manjši graf z notranjim obsegom večjim od g, v katerem mora biti vsak barvni razred barvanja majhen in zaradi tega potrebuje vsaj k barv v vsakem barvanju.

Posplošitve

Lihi notranji obseg in sodi notranji obseg grafa sta dolžini najkrajšega lihega cikla in najkrajšega sodega cikla.

Prek najmanjše dolžine netrivialnega cikla notranji obseg dovoljuje naravne posplošitve 1-sistol ali sistol višjih redov v sistolični geometriji.

Viri

• Brouwer, Andries Evert, Cages (v angleščini), pridobljeno 8. septembra 2010. Elektronski dodatek knjigi Distance-Regular Graphs (Brouwer, Cohen in Neumaier 1989, Springer-Verlag).
• Diestel, Reinhard (2010), Graph Theory (4. izd.), Berlin: Springer-Verlag, ISBN 978-3-642-14278-9
• Erdős, Paul (1959), »Graph theory and probability«, Canadian Journal of Mathematics, 11: 34–38
• Wilson, Robin James; Watkins, John Jaeger (1997), Uvod v teorijo grafov [Graphs : an introductory approach] (Knjižnica Sigma - 63 izd.), Ljubljana: DFMA Slovenije, COBISS 72250368, ISBN 961-212-081-1

Zunanje povezave

• Weisstein, Eric Wolfgang. »Girth«. MathWorld.