Kromatično število

Kromatično število (ali barvnost) grafa G je v teoriji grafov najmanjše število k, za katerega je G k-pobarvljiv, oziroma je najmanjše število barv, s katerimi je mogoče pobarvati graf G po točkah tako, da imajo pari točk poljubne povezave različne barve. Običajno se označuje kot $\chi (G)\!\,$.

• 
  Kromatično število vsakega polnega grafa $K_{n}\!\,$ pri $n\geq 2\!\,$ je $n\!\,$. Na sliki polni graf $K_{12}\!\,$
• 
  Kromatično število hiperkockinega grafa je 2
• 
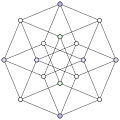
  Kromatično število Desarguesovega grafa je 2
• 
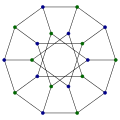
  Kromatično število Ljubljanskega grafa je 2
• 
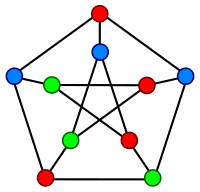
  Kromatično število Fruchtovega grafa je 3
• 
  Kromatično število Biggs-Smithovega grafa je 3
• 
  Kromatično število Higman-Simsovega grafa je 6

Zgled barvanja Petersenovega grafa po točkah. Za njegovo barvanje so potrebne tri različne barve, njegovo kromatično število pa je enako 3.

Viri

• Wilson, Robin James; Watkins, John Jaeger (1997), Uvod v teorijo grafov [Graphs : an introductory approach] (Knjižnica Sigma - 63 izd.), Ljubljana: DFMA Slovenije, COBISS 72250368, ISBN 961-212-081-1