Schwarzev trikotnik
Schwarzev trikotnik je sferni trikotnik s pomočjo katerega se lahko tlakuje sfero.
Imenuje se po nemškem matematiku Hermanu Amandusu Schwarzu (1843–1921).
Schwarzev trikotnik se predstavi s tremi racionalnimi števili v obliki (p q r) kjer vsako število predstavlja kot v oglišču. Vrednost n/d pomeni, da je kot v oglišču n/d-ti del polovice kroga. Vrednost 2 pomeni pravi kot. Kadar števila niso ulomki, se trikotnik imenuje Möbiusov trikotnik, ki odgovarja neprikrivajočemu tlakovanju. Simetrijska grupa se imenuje trikotniška grupa.
Prostor rešitev
urediOsnovna domena trikotnika (p q r) lahko obstaja v različnih prostorih, kar je odvisno od omejitev:
Grafični prikaz
urediSchwarzev trikotnik se lahko prikaže s trikotniškim grafom. Vsak vozel predstavlja rob Schwarzevega trikotnika. Vsak rob je označen z racionalnim številom, ki odgovarja zaporedju zrcaljenja, je enak π/kot ob oglišču
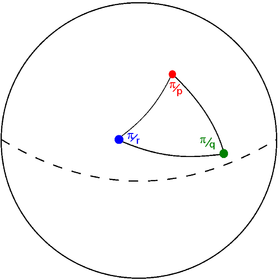 Schwarzev trikotnik (p q r) na sferi. |
 Graf Schwarzevega tikotnika |
Robovi reda 2 predstavljajo pravokotna zrcala, ki se jih lahko izpusti na tej sliki. Coxeter-Dinkinov diagram prikazuje trikotniški graf z robovi reda 2, ki so prikriti.
Za Coxeterjevo grupo se lahko uporabi enostavnejši zapis kot je (p q r) za ciklični graf in (p q 2)=[p, q] (za prave kote) ter (p 2 2) = [p] x [].
Seznam Schwarzevih trikotnikov
urediMöbiusovi trikotniki na sferi
uredi| (2 2 2) ali [2,2] |
(3 2 2) ali [3,2] |
... |
|---|---|---|
| (3 3 2) ali [3,3] |
(4 3 2) ali [4,3] |
(5 3 2) ali [5,3] |
Schwarzevi trikotniki za sfero po gostoti
urediV nadaljevanju so našteti Schwarzevi trikotniki razvrščeni po gostoti (politopski gostoti):
| gostota | Schwarzev trikotnik |
|---|---|
| 1 | (2 3 3), (2 3 4), (2 3 5), (2 2 n) |
| d | (2 2 n/d) |
| 2 | (3/2 3 3), (3/2 4 4), (3/2 5 5), (5/2 3 3) |
| 3 | (2 3/2 3), (2 5/2 5) |
| 4 | (3 4/3 4), (3 5/3 5) |
| 5 | (2 3/2 3/2), (2 3/2 4) |
| 6 | (3/2 3/2 3/2), (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5) |
| 7 | (2 3 4/3), (2 3 5/2) |
| 8 | (3/2 5/2 5) |
| 9 | (2 5/3 5) |
| 10 | (3 5/3 5/2), (3 5/4 5) |
| 11 | (2 3/2 4/3), (2 3/2 5) |
| 13 | (2 3 5/3) |
| 14 | (3/2 4/3 4/3), (3/2 5/2 5/2), (3 3 5/4) |
| 16 | (3 5/4 5/2) |
| 17 | (2 3/2 5/2) |
| 18 | (3/2 3 5/3), (5/3 5/3 5/2) |
| 19 | (2 3 5/4) |
| 21 | (2 5/4 5/2) |
| 22 | (3/2 3/2 5/2) |
| 23 | (2 3/2 5/3) |
| 26 | (3/2 5/3 5/3) |
| 27 | (2 5/4 5/3) |
| 29 | (2 3/2 5/4) |
| 32 | (3/2 5/45/3) |
| 34 | (3/2 3/2 5/4) |
| 38 | (3/2 5/4 5/4) |
| 42 | (5/4 5/4 5/4) |
Trikotniki za evklidsko ravnino
uredi| (3 3 3) |
(4 4 2) |
(6 3 2) |
Gostota 1:
- (3 3 3) – 60-60-60 (enakostranični trikotnik)
- (4 4 2) – 45-45-90 (enakokraki pravokotni trikotnik)
- (6 3 2) – 30-60-90
Trikotniki po gostotah:
- gostota 0: (4 4/3 ∞), (3 3/2 ∞), (6 6/5 ∞)
- gostota 1: (4/3 4/3 2), (4/3 4 2), (6 3/2 2)
- gostota 2: (6/5 3 2), (6 6 3/2), (6 6/5 3)
Trikotniki za hiperbolično ravnino
uredi| (7 3 2) |
(8 3 2) |
(5 4 2) |
| (4 3 3) |
(4 4 3) |
(∞ ∞ ∞) |
| Fundamentalne domene triukotnikov (p q r) | ||
Gostota 1:
- (2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
- (2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
- (2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
- (2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
- (3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
- (3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
- (3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
- (3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
- ...
- (∞ ∞ ∞)
Trikotnik (2 3 7) je najmanjši hiperbolični Schwarzev trikotnik.
Trikotnik (2 3 8) lahko tlakuje Bolzovo ploskev, ki je visoko simetrična ploskev z rodom enakim 2.
Glej tudi
urediZunanje povezave
uredi- Weisstein, Eric Wolfgang. »Schwarz Triangle«. MathWorld.
- Schwarzev trikotnik na WolframAlpha (angleško)


