Arhimedski graf
Arhimedski graf je v teoriji grafov poliedrski graf in tvori skelet arhimedskega telesa. Obstaja 13 arhimedskih grafov in vsi so regularni poliedrski grafi in zaradi tega tudi 3-točkovnopovezani, točkovnoprehodni in ravninski grafi. So tudi Hamiltonovi grafi.[1]:267–270 Eurlerjevi grafi so vsi štirje kvartični grafi: kubooktaedrski, rombikubooktaedrski, ikozidodekaedrski in rombiikozidodekaedrski graf. Povezavnoprehodna sta le kubooktaedrski in ikozidodekaedrski graf.
Poleg 13-ih grafov se med arhimedske grafe lahko šteje tudi neskončna množica prizemskih in antiprizemskih grafov.[1]:261
| ime | graf G (Schleglov diagram) |
stopnja d |
točke V |
povezave E |
red | Aut (G) | |
|---|---|---|---|---|---|
| graf prisekanega tetraedra | 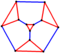 |
3 | 12 | 18 | 24 |
| kubooktaedrski graf |  |
4 | 12 | 24 | 48 |
| graf prisekane kocke |  |
3 | 24 | 36 | 48 |
| graf prisekanega oktaedra | 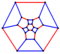 |
3 | 24 | 36 | 48 |
| rombikubooktaedrski graf |  |
4 | 24 | 48 | 48 |
| graf prisekanega kubooktaedra |  |
3 | 48 | 72 | 48 |
| graf prirezane kocke |  |
5 | 24 | 60 | 24 |
| ikozidodekaedrski graf |  |
4 | 30 | 60 | 120 |
| graf prisekanega dodekaedra |  |
3 | 60 | 90 | 120 |
| graf prisekanega ikozaedra | 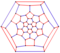 |
3 | 60 | 90 | 120 |
| rombiikozidodekaedrski graf |  |
4 | 60 | 120 | 120 |
| graf prisekanega ikozidodekaedra |  |
3 | 120 | 180 | 120 |
| graf prirezanega dodekaedra |  |
5 | 60 | 150 | 60 |
Glej tudi
urediSklici
urediViri
uredi- Read, Ronald Cedric; Wilson, Robin James (1998), An Atlas of Graphs, Oxford: Clarendon Press, COBISS 8615001, ISBN 0-19-853289-X