Funkcija gama

Fúnkcija gáma (tudi Eulerjeva funkcija gama),je v matematiki specialna funkcija, ki razširja pojem fakultete na kompleksna števila. Zapisa se je domislil Adrien-Marie Legendre, funkcijo samo pa je uvedel Leonhard Euler. Če je realni del kompleksnega števila z pozitiven, potem integral:

Graf funkcije Γ na realni premici

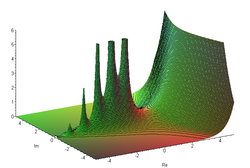Absolutna vrednost funkcije Γ v kompleksni ravnini

Razširjena različica funkcije Γ v kompleksni ravnini

$\Gamma (z)=\int _{0}^{\infty }t^{z-1}\,e^{-t}\,\mathrm {d} t\!\,$

konvergira absolutno. Z integracijo po delih je moč pokazati, da velja:

$\Gamma (z+1)=z\Gamma (z)\!\,.$

Ker je Γ(1) = 1, odtod sledi:

$\Gamma (n+1)=n!\!\,$

za vsa naravna števila n. Z analitičnim nadaljevanjem je moč razširiti Γ(z) v meromorfno funkcijo definirano za vsa kompleksna števila z razen z = 0, −1, −2, −3, ..., kjer ima pol. Funkcija gama se imenuje ta razširjena različica.

Funkcija gama nima ničel. Morda najbolj znana vrednost funkcije gama pri necelih številih je:

$\Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}\!\,.$

Funkcija gama ima pol reda 1 pri z = −n za vsako naravno število n; residuum je tam podan kot:

$\operatorname {Res} (\Gamma ,-n)={\frac {(-1)^{n}}{n!}}\!\,.$

Naslednja multiplikativna oblika funkcije gama velja za vsa kompleksna števila z, ki niso nepozitivna cela števila:

$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n}\!\,.$

Tu je γ Euler-Mascheronijeva konstanta.

Iz funkcionalne enačbe lahko izpeljemo:

${\begin{aligned}\Gamma \left(x\right)&={\frac {\Gamma \left(x+1\right)}{x}}={\frac {\Gamma \left(x+2\right)}{x\left(x+1\right)}}=\ldots \\&={\frac {\Gamma \left(x+k+1\right)}{x\left(x+1\right)\left(x+2\right)\ldots \left(x+k\right)}}\!\,,\end{aligned}}$

od koder sledi, da ima funkcija pri negativnih celih argumentih in pri argumentu enakem 0 pole lihe stopnje.

Posebne vrednosti funkcije Γ

${\begin{array}{lll}\Gamma (-3/2)&={\frac {4{\sqrt {\pi }}}{3}}&\approx 2,363\\\Gamma (-1/2)&=-2{\sqrt {\pi }}&\approx -3,545\\\Gamma (1/2)&={\sqrt {\pi }}&\approx 1,772\\\Gamma (1)&=0!&=1\\\Gamma (3/2)&={\frac {\sqrt {\pi }}{2}}&\approx 0,886\\\Gamma (2)&=1!&=1\\\Gamma (5/2)&={\frac {3{\sqrt {\pi }}}{4}}&\approx 1,329\\\Gamma (3)&=2!&=2\\\Gamma (7/2)&={\frac {15{\sqrt {\pi }}}{8}}&\approx 3,323\\\Gamma (4)&=3!&=6\\\end{array}}$

Zunanje povezave

• Weisstein, Eric Wolfgang. »Gamma Function«. MathWorld.