Sinusni izrek

Sínusni izrèk v ravninski trigonometriji pravi, da je v trikotniku razmerje med sinusom kota in dolžino nasproti ležeče stranice enako za katerikoli par stranic - nasprotni kot.

Sinusni izrek

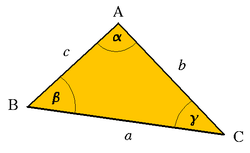
Za trikotnik na desni sliki tako velja zveza:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}$

Zgodovina

Arabski matematik ibn Irak (okoli 970–1036) je dokazal osvobodilni izrek ali zadostni, sposobni izrek, aš-šaklu-l-mukni, kakor so tedaj rekli sinusnemu izreku, najprej za sferno, potem pa še za ravninsko trigonometrijo. Z njim je trigonometrijo osvobodil kroga in štirikotnika, dal ji je preprosti osnovnejši predmet, sestavljen le iz treh, namesto iz štirih točk.

Za poševnokotni trikotnik v sferni trigonometriji je prvi izpeljal in pokazal splošni sinusni izrek:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R\!\,$

arabski matematik in astronom Abul Vefa (940–998). Za njim ga je uporabljal tudi Nasir at-Tusi.

Glej tudi

• kosinusni izrek
• triangulacija