Fourierova transformacija

Fourierova transformacija (natančneje zvezna Fourierova transformacija ; izgovorjava:[fuʁie])) je matematična metoda s področja Fourierove analize, ki aperiodični signal razčleni na neprekinjen spekter. Funkcija, ki opisuje ta spekter, se imenuje tudi Fourierova transformacija ali spektralna funkcija. Gre za integralno transformacijo,o poimenovano po matematiku Jeanu Baptistu Josephu Fourierju. Fourier je leta 1822 uvedel Fourierovo serijo, ki pa je definirana le za periodične signale in vodi do diskretnega frekvenčnega spektra.

Primer uporabe Fourierove transformacije je določanje sestavin zvoka. Ta slika je rezultat uporabe transformacije konstantnega Q (s Fourierjem povezane transformacije) na valovno akorda C-dur na klavirju. Prvi trije vrhovi na levi ustrezajo frekvencam osnovne frekvence akorda (C, E, G). Preostali manjši vrhovi so visokofrekvenčni prizvoki teh osnovnih tonov..

Rdeča sinusna krivulja sinusoid se lahko opiše z amplitudo vrha (1), razdaljo med vrhovoma (2), RMS (3), valovno dolžino (4). Rdeča in modra sinusoida sta zamaknjeni za fazno razliko

θ

.

\scriptstyle f(t)

\scriptstyle {\hat {f}}(\omega )

\scriptstyle g(t)

\scriptstyle {\hat {g}}(\omega )

\scriptstyle t

\scriptstyle \omega

\scriptstyle t

\scriptstyle \omega

zgornja vrsta kaže enotni impulz kot funkcijo časa (

f (t)

) in njegovo Fourierovo translmacijo kot funkcijo frekvence (

f̂ (ω)

). Spodnja vrstica prikazuje zakasnjeni enotni impulz kot funkcijo časa (

g (t)

) in njegovo Fourierjevo transformacijo kot funkcijo frekvence (

ĝ (ω)

). [Zakasnitev v časovni domeni pomeni kompleksni fazni premik v frekvenčni domeni.

Obstaja kar nekaj primerov uporabe, za katere treba za Fourierjevo transformacijo uporabiti računalnik. V ta namen je na voljo diskretna Fourierjeva transformacija ali hitra Fourierjeva transformacija.

Definicija uredi

Naj bo $f\in L^{1}(\mathbb {R} ^{n})$ integrabilna funkcija, kjer $L^{1}$ imenovan Lebesgueov prostor. (Zvezna) Fourierova transformacija ${\mathcal {F}}f$ od $f$ je definirana z

({\mathcal {F}}f)(y)={\frac {1}{{\sqrt {2\pi }}^{\ n}}}\int _{\mathbb {R} ^{n}}f(x)\,\mathrm {e} ^{-\mathrm {i} y\cdot x}\,\mathrm {d} x

in ustrezna inverzna transformacija je:

f(x)={\frac {1}{{\sqrt {2\pi }}^{\ n}}}\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{\mathrm {i} y\cdot x}\,\mathrm {d} y\;.

Pri tem sta $\mathrm {d} x$ in $\mathrm {d} y$ so $n$ -dimenzionalna prostorska elementa, $\mathrm {i}$ imaginarna enota, $y\cdot x$ pa standardni produkt vektorjev $y$ in $x$ .

Normalizacijska konstanta v literaturi ni dosledna. V teoriji psevdodiferencialnih operatorjev in pri obdelavi signalov se faktor $1/(2\pi )^{n/2}$ v transformaciji pogosto izpušča, tako da inverzna transformacija ustrezno dobi na začetek faktor $1/(2\pi )^{n}$ . Transformacija je tako:

({\mathcal {F}}f)(y)=\int _{\mathbb {R} ^{n}}f(x)\,\mathrm {e} ^{-\mathrm {i} y\cdot x}\,\mathrm {d} x\;,

f(x)={\frac {1}{(2\pi )^{n}}}\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{\mathrm {i} y\cdot x}\,\mathrm {d} y\;.

Faktor na začetku faktor preprečuje neposredno uporabo Plancherelovega izreka, ker potem Fourierova transformacija ne daje več unitarne preslikave $L^{1}(\mathbb {R} ^{n})\cap L^{2}(\mathbb {R} ^{n})$ in tako se spremeni moč signala. Vendar, kot pri vseh ortogonalnih transformacijah, je to mogoče zlahka kompenzirati s substitucijo (ponovno skaliranje abscise) in zato ne predstavlja temeljne težave. Točno to predlaga literatura o obdelavi signalov in sistemski teoriji: prehod od naravne frekvence h kotni frekvenci $\omega =2\pi y$ (ki vključuje faktor):

f(x)=\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{2\pi \mathrm {i} y\cdot x}\,\mathrm {d} y\;=\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{\mathrm {i} \omega \cdot x}\,\mathrm {d} y\;.

Realna inačica Fourierove transformacije se imenuje Hartleyjeva transformacija. Za realne funkcije $f$ Fourierovo transformacijo lahko nadomestimo s sinusno in kosinusno transformacijo.

Primeri uporabe uredi

Stiskanje podatkov za digitalno komunikacijo uredi

Stiskanje digitalnih podatkov s pomočjo Fourierove transformacije je osrednja tehnologija na področju komunikacije, izmenjave podatkov in pretakanja medijev na (mobilnem) internetu. ^[1]

Tabele pomembnih Fourierovih transformacij uredi

Naslednje tabele prikazujejo nekaj zaprtih Fourierovih transformacij. Funkciji f(x) in g(x) označimo njuni Fourierovi transformaciji s f̂ in ĝ. Vključene so samo tri najpogostejše konvencije. Morda bi bilo koristno opaziti, da podaja vnos 105 razmerje med Fourierovo transformacijo funkcije in izvirno funkcijo, ki jo je mogoče razumeti kot povezavo Fourierjeve transformacije in njenega obrata.

Funkcionalne relacije, enodimenzionalne uredi

Fourierove transformacije v tej tabeli lahko najdete pri Erdélyi (1954) or Kammler (2000, appendix).

	Funkcija	Fourierova transformacija asbscisa je unitarna običajna frekvenca	Fourierova transformacija unitarna, kotna frekvenca	Fourierova transformacija< ne-unitarna, kotna frekvenca	pripombe
	$f(x)\,$	${\begin{aligned}&{\hat {f}}(\xi )\triangleq {\hat {f}}_{1}(\xi )\\&=\int _{-\infty }^{\infty }f(x)e^{-i2\pi \xi x}\,dx\end{aligned}}$	${\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}}_{2}(\omega )\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)e^{-i\omega x}\,dx\end{aligned}}$	${\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}}_{3}(\omega )\\&=\int _{-\infty }^{\infty }f(x)e^{-i\omega x}\,dx\end{aligned}}$	Definiticije
101	$a\,f(x)+b\,g(x)\,$	$a\,{\hat {f}}(\xi )+b\,{\hat {g}}(\xi )\,$	$a\,{\hat {f}}(\omega )+b\,{\hat {g}}(\omega )\,$	$a\,{\hat {f}}(\omega )+b\,{\hat {g}}(\omega )\,$	Linearnost
102	$f(x-a)\,$	$e^{-i2\pi \xi a}{\hat {f}}(\xi )\,$	$e^{-ia\omega }{\hat {f}}(\omega )\,$	$e^{-ia\omega }{\hat {f}}(\omega )\,$	Pomik v časovni domeni
103	$f(x)e^{iax}\,$	${\hat {f}}\left(\xi -{\frac {a}{2\pi }}\right)\,$	${\hat {f}}(\omega -a)\,$	${\hat {f}}(\omega -a)\,$	Pomik v frekvenčni domeni, dualno vrstici 102
104	$f(ax)\,$	${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\omega }{a}}\right)\,$	${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\omega }{a}}\right)\,$	Skalirano v časovni domeni. Če je ${\|a\|}$ velik, se $f(ax)\,$ koncentrira na 0 in ${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\omega }{a}}\right)\,$ razširi in zniža.
105	${\hat {f_{n}}}(x)\,$	${\hat {f}}_{1}(x)\ {\stackrel {{\mathcal {F}}_{1}}{\longleftrightarrow }}\ f(-\xi )\,$	${\hat {f}}_{2}(x)\ {\stackrel {{\mathcal {F}}_{2}}{\longleftrightarrow }}\ f(-\omega )\,$	${\hat {f}}_{3}(x)\ {\stackrel {{\mathcal {F}}_{3}}{\longleftrightarrow }}\ 2\pi f(-\omega )\,$	Ista transformacija dvakrat zapored, x po prvi transformaciji nastopi namesto frekvence (ξ or ω).
106	${\frac {d^{n}f(x)}{dx^{n}}}\,$	$(i2\pi \xi )^{n}{\hat {f}}(\xi )\,$	$(i\omega )^{n}{\hat {f}}(\omega )\,$	$(i\omega )^{n}{\hat {f}}(\omega )\,$	Odvod n-tega reda. $f$ je Schwartzova funkcija
	$\int _{-\infty }^{x}f(\tau )d\tau$	${\frac {{\hat {f}}(\xi )}{i2\pi \xi }}+C\,\delta (\xi )$			Integracija.^[2] Opomba: $\delta$ je Diracova delta funkcija in $C$ povprečna (DC) vrednost $f(x)$ , tako da je $\int _{-\infty }^{\infty }(f(x)-C)\,dx=0$
107	$x^{n}f(x)\,$	$\left({\frac {i}{2\pi }}\right)^{n}{\frac {d^{n}{\hat {f}}(\xi )}{d\xi ^{n}}}\,$	$i^{n}{\frac {d^{n}{\hat {f}}(\omega )}{d\omega ^{n}}}$	$i^{n}{\frac {d^{n}{\hat {f}}(\omega )}{d\omega ^{n}}}$	To je dualno vrstici 106
108	$(f*g)(x)\,$	${\hat {f}}(\xi ){\hat {g}}(\xi )\,$	${\sqrt {2\pi }}{\hat {f}}(\omega ){\hat {g}}(\omega )\,$	${\hat {f}}(\omega ){\hat {g}}(\omega )\,$	Izraz $f * g$ pomeni konvolucijo $f$ in $g$ — to pravilo je t.i. konvolucijski teorem
109	$f(x)g(x)\,$	$\left({\hat {f}}*{\hat {g}}\right)(\xi )\,$	${\frac {1}{\sqrt {2\pi }}}\left({\hat {f}}*{\hat {g}}\right)(\omega )\,$	${\frac {1}{2\pi }}\left({\hat {f}}*{\hat {g}}\right)(\omega )\,$	To je dualno 108
110	For $f (x)$ purely real	${\hat {f}}(-\xi )={\overline {{\hat {f}}(\xi )}}\,$	${\hat {f}}(-\omega )={\overline {{\hat {f}}(\omega )}}\,$	${\hat {f}}(-\omega )={\overline {{\hat {f}}(\omega )}}\,$	Hermitska simetrija $z$ zahteva kompleksni konjugat.
113	Za imaginarno $f (x)$	${\hat {f}}(-\xi )=-{\overline {{\hat {f}}(\xi )}}\,$	${\hat {f}}(-\omega )=-{\overline {{\hat {f}}(\omega )}}\,$	${\hat {f}}(-\omega )=-{\overline {{\hat {f}}(\omega )}}\,$	$z$ pomeni kompleksni konjugat.
114	${\overline {f(x)}}$	${\overline {{\hat {f}}(-\xi )}}$	${\overline {{\hat {f}}(-\omega )}}$	${\overline {{\hat {f}}(-\omega )}}$	[[<kompleksna konjugacija]], generalizacija 110 in 113
115	$f(x)\cos(ax)$	${\frac {{\hat {f}}\left(\xi -{\frac {a}{2\pi }}\right)+{\hat {f}}\left(\xi +{\frac {a}{2\pi }}\right)}{2}}$	${\frac {{\hat {f}}(\omega -a)+{\hat {f}}(\omega +a)}{2}}\,$	${\frac {{\hat {f}}(\omega -a)+{\hat {f}}(\omega +a)}{2}}$	Slledi iz 101 in 103 s pomočjo Eulerjeve formule: $\cos(ax)={\frac {e^{iax}+e^{-iax}}{2}}.$
116	$f(x)\sin(ax)$	${\frac {{\hat {f}}\left(\xi -{\frac {a}{2\pi }}\right)-{\hat {f}}\left(\xi +{\frac {a}{2\pi }}\right)}{2i}}$	${\frac {{\hat {f}}(\omega -a)-{\hat {f}}(\omega +a)}{2i}}$	${\frac {{\hat {f}}(\omega -a)-{\hat {f}}(\omega +a)}{2i}}$	Sledi iz 101 in 103 s pomočjo Eulerjeve formule: $\sin(ax)={\frac {e^{iax}-e^{-iax}}{2i}}.$

kvadratno integrabilne funkcije, enodimenzionalne uredi

Fourierove transformacije v tej tabeli je najti v Campbell & Foster (1948), Erdélyi (1954), ali Kammler (2000, priloga).

	Funkcija	Fourierova transformacija asbscisa je unitarna običajna frekvenca	Fourierova transformacija unitarna, kotna frekvenca	Fourierova transformacija< ne-unitarna, kotna frekvenca	pripombe
	$f(x)\,$	${\begin{aligned}&{\hat {f}}(\xi )\triangleq {\hat {f}}_{1}(\xi )\\&=\int _{-\infty }^{\infty }f(x)e^{-i2\pi \xi x}\,dx\end{aligned}}$	${\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}}_{2}(\omega )\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)e^{-i\omega x}\,dx\end{aligned}}$	${\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}}_{3}(\omega )\\&=\int _{-\infty }^{\infty }f(x)e^{-i\omega x}\,dx\end{aligned}}$	Definicije
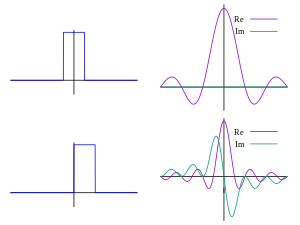
201	$\operatorname {rect} (ax)\,$	${\frac {1}{\|a\|}}\,\operatorname {sinc} \left({\frac {\xi }{a}}\right)$	${\frac {1}{\sqrt {2\pi a^{2}}}}\,\operatorname {sinc} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{\|a\|}}\,\operatorname {sinc} \left({\frac {\omega }{2\pi a}}\right)$	Pravokotni pulz in normalizirana sinc funkcija, definirana kot $sinc(x) = sin(π x) / π x$
202	$\operatorname {sinc} (ax)\,$	${\frac {1}{\|a\|}}\,\operatorname {rect} \left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\sqrt {2\pi a^{2}}}}\,\operatorname {rect} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{\|a\|}}\,\operatorname {rect} \left({\frac {\omega }{2\pi a}}\right)$	Dualno vrstici 201.
203	$\operatorname {sinc} ^{2}(ax)$	${\frac {1}{\|a\|}}\,\operatorname {tri} \left({\frac {\xi }{a}}\right)$	${\frac {1}{\sqrt {2\pi a^{2}}}}\,\operatorname {tri} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{\|a\|}}\,\operatorname {tri} \left({\frac {\omega }{2\pi a}}\right)$	$tri(x)$ je trikotna funkcija
204	$\operatorname {tri} (ax)$	${\frac {1}{\|a\|}}\,\operatorname {sinc} ^{2}\left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\sqrt {2\pi a^{2}}}}\,\operatorname {sinc} ^{2}\left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{\|a\|}}\,\operatorname {sinc} ^{2}\left({\frac {\omega }{2\pi a}}\right)$	Dualno vrstici 203.
205	$e^{-ax}u(x)\,$	${\frac {1}{a+i2\pi \xi }}$	${\frac {1}{{\sqrt {2\pi }}(a+i\omega )}}$	${\frac {1}{a+i\omega }}$	Funkcija $u (x)$ je Heavisidov prag in $a > 0$ .
206	$e^{-\alpha x^{2}}\,$	${\sqrt {\frac {\pi }{\alpha }}}\,e^{-{\frac {(\pi \xi )^{2}}{\alpha }}}$	${\frac {1}{\sqrt {2\alpha }}}\,e^{-{\frac {\omega ^{2}}{4\alpha }}}$	${\sqrt {\frac {\pi }{\alpha }}}\,e^{-{\frac {\omega ^{2}}{4\alpha }}}$	Za unitarne Fourierove tranasformacije je torej $e - αx 2$ svoja lastna transformacija - do multiplikatorja $α$ . Da to velja, mora biti $Re(α) > 0$ .
208	$e^{-a\|x\|}\,$	${\frac {2a}{a^{2}+4\pi ^{2}\xi ^{2}}}$	${\sqrt {\frac {2}{\pi }}}\,{\frac {a}{a^{2}+\omega ^{2}}}$	${\frac {2a}{a^{2}+\omega ^{2}}}$	Za $Re(a) > 0$ . Fourierova transformacija eksponentne padajoče funkcije je Lorentzova funkcija .
209	$\operatorname {sech} (ax)\,$	${\frac {\pi }{a}}\operatorname {sech} \left({\frac {\pi ^{2}}{a}}\xi \right)$	${\frac {1}{a}}{\sqrt {\frac {\pi }{2}}}\operatorname {sech} \left({\frac {\pi }{2a}}\omega \right)$	${\frac {\pi }{a}}\operatorname {sech} \left({\frac {\pi }{2a}}\omega \right)$	Hyperbolična funkcija si je lastna Fourtierova transformacija
210	$e^{-{\frac {a^{2}x^{2}}{2}}}H_{n}(ax)\,$	${\frac {{\sqrt {2\pi }}(-i)^{n}}{a}}e^{-{\frac {2\pi ^{2}\xi ^{2}}{a^{2}}}}H_{n}\left({\frac {2\pi \xi }{a}}\right)$	${\frac {(-i)^{n}}{a}}e^{-{\frac {\omega ^{2}}{2a^{2}}}}H_{n}\left({\frac {\omega }{a}}\right)$	${\frac {(-i)^{n}{\sqrt {2\pi }}}{a}}e^{-{\frac {\omega ^{2}}{2a^{2}}}}H_{n}\left({\frac {\omega }{a}}\right)$	$H n$ je Hermiteov polinom $n$ tega reda. Če velja $a = 1$ , so Gauss-Hermiteove funkcije lastne funkcije Fourierovega operatorja. Enačba se poenostavi na 206 za $n = 0$ .

Dvodimenzionalne funkcije uredi

	Function	Fourier transform unitary, ordinary frequency	Fourier transform unitary, angular frequency	Fourier transform non-unitary, angular frequency	Remarks
400	$f(x,y)$	${\begin{aligned}&{\hat {f}}(\xi _{x},\xi _{y})\triangleq \\&\iint f(x,y)e^{-i2\pi (\xi _{x}x+\xi _{y}y)}\,dx\,dy\end{aligned}}$	${\begin{aligned}&{\hat {f}}(\omega _{x},\omega _{y})\triangleq \\&{\frac {1}{2\pi }}\iint f(x,y)e^{-i(\omega _{x}x+\omega _{y}y)}\,dx\,dy\end{aligned}}$	${\begin{aligned}&{\hat {f}}(\omega _{x},\omega _{y})\triangleq \\&\iint f(x,y)e^{-i(\omega _{x}x+\omega _{y}y)}\,dx\,dy\end{aligned}}$	Spremenljivke $ξ x$ , $ξ y$ , $ω x$ , $ω y$ so realna števila. Področje integrala je celotna ravnina.
401	$e^{-\pi \left(a^{2}x^{2}+b^{2}y^{2}\right)}$	${\frac {1}{\|ab\|}}e^{-\pi \left({\frac {\xi _{x}^{2}}{a^{2}}}+{\frac {\xi _{y}^{2}}{b^{2}}}\right)}$	${\frac {1}{2\pi \,\|ab\|}}e^{-{\frac {1}{4\pi }}\left({\frac {\omega _{x}^{2}}{a^{2}}}+{\frac {\omega _{y}^{2}}{b^{2}}}\right)}$	${\frac {1}{\|ab\|}}e^{-{\frac {1}{4\pi }}\left({\frac {\omega _{x}^{2}}{a^{2}}}+{\frac {\omega _{y}^{2}}{b^{2}}}\right)}$	Obe funkciji sta gaussovi, lahko da brez prostornine = 1
402	$\operatorname {circ} \left({\sqrt {x^{2}+y^{2}}}\right)$	${\frac {J_{1}\left(2\pi {\sqrt {\xi _{x}^{2}+\xi _{y}^{2}}}\right)}{\sqrt {\xi _{x}^{2}+\xi _{y}^{2}}}}$	${\frac {J_{1}\left({\sqrt {\omega _{x}^{2}+\omega _{y}^{2}}}\right)}{\sqrt {\omega _{x}^{2}+\omega _{y}^{2}}}}$	${\frac {2\pi J_{1}\left({\sqrt {\omega _{x}^{2}+\omega _{y}^{2}}}\right)}{\sqrt {\omega _{x}^{2}+\omega _{y}^{2}}}}$	Funkcija je definirana $circ(r) = 1$ za $0 \leq r \leq 1$ , sicer pa = 0. Rezultat je porazdelitev amplitud za Airyjev disk

Glej tudi uredi

Diskretna Fourierjeva transformacija
Fourierjeva transformacija za signale z diskretnim časom
Hitra Fourierjeva transformacija
Inverzna hitra Fourierjeva transformacija

Literatura uredi

Spletne povezave uredi

Sklici uredi

↑ Martin Donner (2006). »Fouriers Beitrag zur Geschichte der Neuen Medien« (PDF). Humboldt-Universität zu Berlin (v nemščini). Pridobljeno 30. julija 2021.
↑ »Integracija kot lastnost Foourierove transformacije«. The Fourier Transform .com. 2015 [2010]. Arhivirano iz spletišča dne 26. januarja 2022. Pridobljeno 20. avgusta 2023.

[1] Martin Donner (2006). »Fouriers Beitrag zur Geschichte der Neuen Medien« (PDF). Humboldt-Universität zu Berlin (v nemščini). Pridobljeno 30. julija 2021.

[2] »Integracija kot lastnost Foourierove transformacije«. The Fourier Transform .com. 2015 [2010]. Arhivirano iz spletišča dne 26. januarja 2022. Pridobljeno 20. avgusta 2023.

[1]

[2]