Ukrivljenost

Ukrívljenost (oznaka $\kappa \,$) v matematiki pove koliko geometrijski objekt odstopa od ravnosti, kot se jo pozna pri premici. V ravnini je ukrivljenost skalarna količina, v treh ali več razsežnostih je ukrivljenost določena z vektorjem ukrivljenosti, ki upošteva razen smeri še ostrino ukrivljenosti. Pri kompleksnejših objektih se določa ukrivljenost z zapletenimi pojmi iz linearne algebre, kot je na primer Riemannov tenzor ukrivljenosti. Ločiti pa je treba med notranjo in zunanjo ukrivljenostjo. Zunanja ukrivljenost je definirana za objekte, ki so potopljeni v druge prostore (običajno v evklidski prostor) tako, da je ukrivljenost povezana s polmerom krožnice, ki je pritisnjena h krivulji. Notranja ukrivljenost pa je definirana v vsaki točki Riemannove mnogoterosti. V nadaljevanju je opisana zunanja ukrivljenost.

Na krivuljo $C\,$ pritisnjena krožnica.

Ukrivljenost ravninskih krivulj

Uporabljata se vsaj dva načina za opis ukrivljenosti. Prvi način je geometrijski, drugi pa fizikalni.

Naj bo $C\,$ ravninska krivulja. Ukrivljenost te krivulje v določeni točki je merilo občutljivosti tangente pri premiku od te do naslednje točke.

Po geometrijskem načinu je ukrivljenost premice enaka nič. Ukrivljenost krožnice je velika, če je polmer krožnice $R\,$ majhen in obratno. Torej se lahko zapiše:

$\kappa ={\frac {1}{R}}\!\,.$.

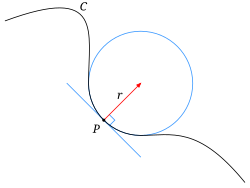
Za dano krivuljo $C\,$ in točko $P\,$ na njej obstaja krožnica, ki se najbolj prilega krivulji v okolici točke $P\,$. Ta krožnica se imenuje pritisnjena krožnica v točki $P\,$. Ukrivljenost v točki $P\,$ je definirana s to krožnico.

Po fizikalnem načinu razumevanja pojma se najprej predpostavi, da se telo giblje vzdolž krivulje z enotsko hitrostjo. Če se vzame čas kot parameter krivulje $C\,$, to nudi naravno parametrizacijo krivulje. Enotski tangentni vektor naj bo označen s $T\,$ in je odvisen tudi od časa. Ukrivljenost je v tem primeru stopnja spreminjanja vektorja $T\,$ ali:

$\kappa =\left\|{\frac {\mathrm {d} \mathbf {T} }{\mathrm {d} s}}\right\|\!\,.$

Ta izraz pomeni velikost pospeška telesa (delca). Geometrijsko to pomeni hitrost vrtenja tangentnega vektorja. Kadar se smer krivulje ne spreminja veliko, ostane enotski tangentni vektor enak in krivulja ima majhno ukrivljenost.

Prikazana sta vektorja T in N, ki skupaj tvorita osnovni sistem. Vektorja sta prikazana v dveh točkah ravninske krivulje, vidi se sprememba vektorja T pri prehodu do druge točke, ki je samo premaknjena oblika prvega okvirja. V drugi točki, ki jo opisuje premaknjena oblika prvega okvirja, je nastala spremeba vektorja T v velikosti T: δT' kjer je δs razdalja med točkama. V limiti bi imel ${\tfrac {d\mathbf {T} }{ds}}$ enako smer kot N in tako ukrivljenost opisuje hitrost vrtenja osnovnega sistema.

Točnejša definicija

Naj bo $C\,$ zvezno odvedljiva ravninska krivulja za katero velja, da je zanjo znana parametrična enačba kot par funkcij $y(t)=(x(t),y(t))\,$, ki imata zvezni prvi in drugi odvod, da je po celotni domeni:

$\|\gamma '\|^{2}=x'(t)^{2}+y'(t)^{2}\not =0\!\,.$

Za takšno ravninsko krivuljo obstoja parametrizacija z ločno dolžino tako, da velja:

$\|\gamma '\|^{2}=x'(s)^{2}+y'(s)^{2}=1\!\,.$

Vektor hitrosti T(s) je enotski tangentni vektor.

Enotski normalni (pravokotni) vektor je dan z:

$\mathbf {T} (s)=\gamma '(s)\!\,.$

Ukrivljenost $\kappa (s)\,$ se izračuna kot:

$\kappa (s)=\|\mathbf {T} '(s)\|=\|\gamma ''(s)\|=\left|k(s)\right|\!\,,$

kjer je:

• $k(s)\,$ usmerjena ali orientirana ukrivljenost s predznakom.

Polmer ukrivljenosti $R(s)\,$ pa se izračuna po obrazcu:

$R(s)={\frac {1}{\kappa (s)}}\!\,.$

Za ravninsko krivuljo, ki je dana parametrično v kartezičnem koordinatnem sistemu kot $y(t)=(x(t),y(t))\,$, je ukrivljenost enaka:

$\kappa ={\frac {|x'y''-y'x''|}{(x'^{2}+y'^{2})^{3/2}}}\,$ (s črtico so označeni odvodi po parametru $t\,$). Iz tega se dobi predznačeno ukrivljenost $k\,$ kot:

$k={\frac {x'y''-y'x''}{(x'^{2}+y'^{2})^{3/2}}}\!\,.$

To se lahko izrazi na način, ki je neodvisen od koordinatnega sistema:

$k={\frac {\det(\gamma ',\gamma '')}{\|\gamma '\|^{3}}},\ \ \ \kappa ={\frac {|\det(\gamma ',\gamma '')|}{\|\gamma '\|^{3}}}\!\,.$

Zgled

Za zgled naj bo parabola z enačbo $y=x^{2}\,$. Enačbo se lahko parametrizira z $y(t)=(t,t^{2})=(x,y)\,$. Odvodi so:

$x'=1,\quad x''=0,\quad y'=2t,\quad y''=2\!\,.$

Iz tega se dobi:

$\kappa (t)=\left|{\frac {x'y''-y'x''}{({x'^{2}+y'^{2}})^{3/2}}}\right|={\frac {1\cdot 2-(2t)(0)}{(1+(2t)^{2})^{3/2}}}={\frac {2}{(1+4t^{2})^{3/2}}}\!\,.$

Ukrivljenost prostorskih krivulj

Naj bo $C\,$ prostorska krivulja v vsaj treh razsežnostih. Ukrivljenost je pospešek telesa, ki se giblje z enotsko hitrostjo vzdolž krivulje. Če se z $y(s)\,$ označi parametrizacijo krivulje $C\,$, potem je enotski tangentni vektor $T(s)\,$ dan z:

$\mathbf {T} (s)=\gamma '(s)\!\,.$

Ukrivljenost pa je velikost pospeška telesa (delca), ki se z enotsko hitrostjo giblje vzdolž krivulje. Če se z dolžino loka $s\,$ parametrizira krivuljo $C\,$, potem je enotski tangentni vektor $T(s)\,$ podan z:

$\mathbf {T} (s)=\gamma '(s)\!\,.$

Ukrivljenost pa je podana z velikostjo pospeška:

$\kappa (s)=\|\mathbf {T} '(s)\|=\|\gamma ''(s)\|\!\,.$

Smer pospeška je enotski normalni vektor $N(s)\,$, ki je določen z:

$\mathbf {N} (s)={\frac {\mathbf {T} '(s)}{\|\mathbf {T} '(s)\|}}\!\,.$

Ravnina, ki vsebuje dva vektorja $T(s)\,$ in $N(s)\,$, se imenuje oskulacijska ali pritisnjena ravnina na krivuljo v točki $y(s)\,$. Ukrivljenost se lahko geometrijsko pojasni na naslednji način: Obstoja krožnica v pritisnjeni ravnini tangente v $y(s)\,$ za katero se Taylorjeva vrsta do drugega reda ujema z $y(s)\,$. To pa je oskulacijska krožnica pritisnjena ob krivuljo. Polmer krožnice $R(s)\,$ se imenuje polmer ukrivljenosti in ukrivljenost je obratna vrednost polmera ukrivljenosti, kar je enako:

$\kappa (s)={\frac {1}{R(s)}}\!\,.$

Tangenta , ukrivljenost in normalni vektor opisujejo obnašanje krivulje v bližini dane točke. V treh razsežnostih se obnašanje krivulje lahko opiše s pojmom torzija (glej vzvoj), ki meri kakšna je torzijska ukrivljenost ali zvitost. Krivulja je ravninska, če je njena torzijska ukrivljenost oziroma zvitost enaka 0. Torzija in ukrivljenost sta povezani z Frenet-Serretovimi obrazci in posplošitvami na višje razsežnosti. Torzijska ukrivljenost meri odstopanje krivulje od tega, da bi bila ravninska.

Sedlasta ploskev z normalnimi ravninami v smereh glavnih krivulj.

Ukrivljenost prostora in višje razsežnosti

Tudi tri in mnogorazsežni prostor je lahko ukrivljen (glej ukrivljenost Riemannovih mnogoterosti).

Po odkritju notranje ukrivljenosti, ki je močno povezana z neevklidsko geometrijo so se mnogi matematiki in znanstveniki spraševali, če je fizični prostor ukrivljen. Mnogi so trdili, da bi morala biti ukrivljenost astronomsko velika. V splošni teoriji relativnosti se je to posplošilo z ukrivljenostjo prostor-časa. V relativnostni teoriji je prostor-čas psevdo-Riemannnova mnogoterost. Ko je enkrat časovna koordinata določena, je trirazsežni prostor v tem trenutku ukrivljena Riemannova mnogoterost.

Čeprav je ukrivljen prostor zelo težko opisati, je ukrivljenost prostora krajevno izotropna in homogena, ki se jo lahko opiše z eno Gaussovo krivuljo kot za ploskev. To je zelo strog pogoj, toda odgovarja resnični fizikalni predpostavki, da se točke v različnih smereh med seboj ne razlikujejo.

Pozitivna ukrivljenost pripada obratni vrednosti kvadrata polmera ukrivljenosti. Primer je sfera oziroma hipersfera. Primer negativno ukrivljenega prostora je hiperbolična geometrija. Prostor ali prostor-čas, ki ima ukrivljenost enako 0, je raven. Primer ravnega prostora je evklidski prostor, primer ravnega prostor-časa pa je prostor Minkowskega (imenuje se po nemškem matematiku Hermannu Minkowskem (1864 – 1909).).

Vzporedni prenos vektorja od A → N → B da drugi vektor. Nemožnost vrnitve na začetni vektor se meri s holonomijo ploskve.

Posplošitev

Pojem ukrivljenosti se lahko definira tudi v splošnejšem okolju Mnoge od teh posplošitev poudarjajo različne poglede na ukrivljenost, ki so običajne v nižjih razsežnostih.

Ena izmed takšnih posplošitev je kinematska. Ukrivljenost se v njej obravnava kot kinematska količina, ki jo predstavlja sila, ki jo čuti opazovalec, ki se giblje vzdolž krivulje. Lahko se reče, da se na ukrivljenost lahko gleda kot vrsto plimske sile.

Druga vrsta posplošitve je vzporednega prenosa po ploskvi. To se opiše na naslednji način: če se premika vektor po zaprti zanki na površini sfere tako, da vektor ostane vzporeden, potem končna lega vektorja ni enaka kot začetna. Ta pojav se imenuje holonomija. Različne posplošitve prevzemajo v abstraktni obliki ta način razmišljanja kot merilo za določanje holonomije. Precej podoben pojem ukrivljenosti izhaja iz umeritvene teorije v fiziki, kjer ukrivljenost predstavlja obseg. Vektorski potencial je za obseg količina, ki je odvisna od poti. Lahko se spremeni, če se opazovalec giblje naokoli po zanki.

Znani sta še dve posplošitvi pojma ukrivljenosti. Prva je skalarna ukrivljenost, druga pa je Riccijeva ukrivljenost (imenovana po italijanskem matematiku Gregoriu Ricci-Curbastru (1853 – 1925)). Na ukrivljeni ploskvi, kot je sfera, se ploščina kroga razlikuje od ploščine kroga v ravnem prostoru. Ta razlika se meri s skalarno ukrivljenostjo. Razlika v ploščini krožnega izseka pa se meri z Riccijevo ukrivljenostjo. Skalarno in Riccijevo ukrivljenost se lahko definira na podoben način v treh ali več razsežnostih. Obe sta pomembni v teoriji relativnosti, kjer obe nastopata v Einsteinovih enačbah polja. Te enačbe opisujejo geometrijo prostor-časa. Te posplošitve tvorijo osnovo za predstavo, da je ukrivljenost značilnost mere.

Glej tudi

• krivulja
• diferencialna geometrija krivulj
• stopnja ukrivljenosti
• dioptrija

Zunanje povezave

• Weisstein, Eric Wolfgang. »Curvature«. MathWorld.
• Ukrivljenost ravninske krivulje Arhivirano 2010-12-17 na Wayback Machine. na PlanetMath (angleško)
• Ukrivljenost prostorske krivulje Arhivirano 2012-04-09 na Wayback Machine. na PlanetMath (angleško)
• Ukrivljenost Arhivirano 2011-09-13 na Wayback Machine. na Applet-Magic. com (angleško)
• Dolžina loka in ukrivljenost prostorskih krivulj (angleško)
• Ukrivljenost Arhivirano 2011-05-06 na Wayback Machine. (angleško)