Gama (mrk)

Gama mrka (označena z γ) opiše, kako centralno seka senca Lune ali Zemlje drugo telo. Razdalja, ki se meri v trenutku, ko senčni stožec prečka najbližje središču Zemlje ali Lune, se označi kot delež ekvatorialnega polmera Zemlje ali Lune.

Gama popolnega sončevega mrka. Ilustracija prikazuje gamo sončevega mrka: Rdeča črta kaže najkrajšo razdaljo od središča Zemlje, v tem primeru okoli 75 % Zemljinega polmera. Ker senca prečka severno od središča Zemlje, je gama v tem primeru +0,75.

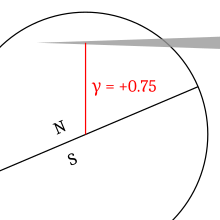
Predznak

Predznak game definira za sončev mrk položaj sence: ali je severno do središča Zemlje ali pa južno. Pri tem sever vedno pomeni pozitivno vrednost. Zemlja je razdeljena na polovici na podlagi kraja, kjer je Sonce v zenitu (torej se spreminja z letnimi časi in se ne nanaša direktno na Zemljine tečaje ali ekvator; torej je Zemljino središče tam, kjer je Sonce neposredno v zenitu).

Za lunin mrk pa znak definira, kje prečka os Zemljino senco, kjer pozitivna vrednost ravno obratno pomeni jug.

Mejni primeri za sončeve mrke na Zemlji

Absolutna vrednost game (označimo jo z |γ|) nam pomaga razločiti različne tipe sončevih mrkov iz Zemlje:

Če bi bila Zemlja krogla, bi bila meja za centralni mrk 1,0, a zaradi geoidne oblike Zemlje (ki povzroči, da je razdalja med poloma rahlo krajša, kot če bi bila Zemlja okrogla) je ta vrednost enaka 0,9972.

• Če je |γ| enak 0, potem je os senčnega stožca natančno med severno in južno polovico s soncem obsijane strani Zemljo, ko gre Luna naravnost skozi središče.
• Če je |γ| manjši kot 0,9972, potem je ta mrk centralni ali središčni. Os senčnega stožca seka Zemljo in na Zemlji obstajajo kraji, kjer je Luna v središču Sonca. Središčni mrki so lahko torej le popolni in kolobarjasti (a če se del sence le komaj dotakne površine Zemlje, se lahko tip spremeni med mrkom iz kolobarjastega v popolnega in obratno; tak pojav imenujemo hibridni mrk).
• Če je |γ| med 0,9972 in 1,0260, potem os senčnega stožca zgreši Zemljo, a ker imata senca in polsenca neničelno širino, se lahko dela sence in polsence stakneta na polarnih območjih Zemlje. Takšen pojav imenujemo ne-središčni popolni ali kolobarjasti mrk.
• Če leži |γ| med 0,9972 in 1,0260 in se posebni primeri, ki so omenjeni zgoraj, ne zgodijo, ali če je |γ| večji kot 1,0260 a manj kot približno 1,55, je mrk delni. Zemlja prepotuje samo polsenco.
• Če |γ| prekorači približno 1,55, potem senčni stožec Zemljo popolnoma zgreši. Ne zgodi se noben mrk.

Sončev mrk 29. aprila 2014 z gamo 0,9999 je primer posebnega primera ne-središčnega kolobarjastega mrka. Os senčnega stožca je komaj opazno zgrešila Zemljin južni pol. Torej se ni dalo določiti nobene centralne črte za območje kolobarjaste vidljivosti.

Naslednji ne-središčni mrk 21. stoletja bo popolni sončev mrk 9. aprila 2043.

Mejni primeri za lunine mrke na Luni glede na Zemljino senco in polsenco

Obstajajo tri vrste luninih mrkov:

• Polsenčni lunin mrk = Luna prečka Zemljino polsenco, senca pa Luno zgreši.
• Delni lunin mrk = Luna prečka Zemljino senco, a ne popolno.
• Popolni lunin mrk = Luna popolno prečka Zemljino senco.

Mejne vrednosti game so torej:

• Če je |γ| enak 0, potem Lunino središče prečka Zemljino senco natančno po sredini.
• Če je |γ| manjši kot 0,2725, potem je ta lunin mrk središčni.
• Če je |γ| med 0,2725 in 0,47, potem je ta lunin mrk popolni.
• Če je |γ| med 0,43 in 1,026, potem je lunin mrk delni.
• Če je |γ| med 0,9871 in 1,0254, potem je ta lunin mrk popolni polsenčni.
• Če je |γ| med 1,026 in približno 1,55, potem je ta lunin mrk polsenčni, kjer Luna potuje samo skozi Zemljino polsenco.
• Če |γ| prekorači približno 1,55, potem Zemljina polsenca popolnoma zgreši Luno, torej se mrk ne zgodi.